| 综合上文的分析可以得到(1)式,
 (1) (1)
所谓投保人的风险溢价,就是指投保人的支付与实际期望损失的差额。这部分差额就形成了风险溢价,其实质就是投保人为了规避自己风险所做的支出。因此,在这里投保人净支付为 ,期望损失为 ,期望损失为 ,因此风险溢价为: ,因此风险溢价为: 。 。
将 变形为 变形为 ,关于 ,关于 泰勒展开 泰勒展开
 略去高阶项,化简为: 略去高阶项,化简为:
 (2) (2)
对 变形为 变形为 ,关于 ,关于 泰勒展开 泰勒展开
 (3) (3)
略去高阶项,结合(2)与(3),由(1)得到:
 (4) (4)
(4)式表示出投保人能够接受的风险溢价区间,同时得出投保人可以接受的保费为:
 (5) (5)
然而,在实务中保险人定价指的是保险费率的确定,因此将(5)式变形为:
 (6) (6)
通过(6)式,就可以很好的看出投保人对于在一定的保险金额下的费率的选择区间。其中, 是普拉特指标,值越大,说明对风险的厌恶程度越大。那么,在投保额一定的条件下,当投保人越厌恶风险,他能够接受的费率区间越大,同时根据(4)式可以说明投保人能接受的最大溢价也就相应变大。所以,投保人越是厌恶风险,就会付出越高的代价来规避风险所带来的损失。 是普拉特指标,值越大,说明对风险的厌恶程度越大。那么,在投保额一定的条件下,当投保人越厌恶风险,他能够接受的费率区间越大,同时根据(4)式可以说明投保人能接受的最大溢价也就相应变大。所以,投保人越是厌恶风险,就会付出越高的代价来规避风险所带来的损失。
(二)保险人的风险溢价
假设 是保险人初始资产, 是保险人初始资产, 是保险人收取的保费,并且保险人全额赔付,同样假设保险人是具有风险规避的效用函数,如图2所示。其中横坐标表示保险人的财产,纵坐标表示保险人的效用。 是保险人收取的保费,并且保险人全额赔付,同样假设保险人是具有风险规避的效用函数,如图2所示。其中横坐标表示保险人的财产,纵坐标表示保险人的效用。
保险人承保后的效用大于他没有承保的效用,否则的话保险人是不会承保的,即: 。又由于保险人的效用函数是风险规避的,由Jensen不等式可知,保险人承保后的期望效用小于保险人承保后期望值的效用,即: 。又由于保险人的效用函数是风险规避的,由Jensen不等式可知,保险人承保后的期望效用小于保险人承保后期望值的效用,即: 。考虑保险人的风险溢价,为收取的保费与期望赔付的差额: 。考虑保险人的风险溢价,为收取的保费与期望赔付的差额: 。 。
 
图2保险人效用分析
经上述分析,必然存在下述不等式:
 (7) (7)
对式 ,将其右端关于 ,将其右端关于 泰勒展开得到: 泰勒展开得到:

略去高阶项,化简得到:
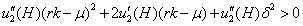
设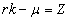 且 且 : :
 (8) (8)
设 是(8)式的两个根,由于 是(8)式的两个根,由于 ,那么必然存在两个正根,可以解得 ,那么必然存在两个正根,可以解得 : :

使得不等式(8)成立的必要条件为:

保险人的溢价区间为:
 (9) (9)
因此,保险人对于保费的制定必须在上述溢价区间内,否则保险人是不会承担保险的:
 (10) (10)
相应的保险费率为:
 (11) (11)
通过(11)式的分析可以发现,保险人制定保险费率的是根据保险人所面对自身的风险态度所决定的。
为了分析方便,设函数
 , ,
其中 ,对 ,对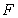 关于 关于 求导数,得到: 求导数,得到:
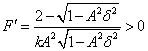 , ,
因此随着 增大,费率 增大,费率 的最小值是增大的。因此保险人的风险态度上就是:在保额不变的情况下,随着保险人厌恶风险程度的增大,费率也相应变大,从而保险人的风险溢价也就变大。 的最小值是增大的。因此保险人的风险态度上就是:在保额不变的情况下,随着保险人厌恶风险程度的增大,费率也相应变大,从而保险人的风险溢价也就变大。
(三)全额赔付下的合同成立条件
对于投保人的合同成立条件有(5),(6)式,对于保险人的合同成立条件有(10),(11)式,综合上面,得到:

那么,可以得到合同成立的费率区间:
 。 。
在这样的条件成立下,可以看出来随着投保人与保险人各自的风险态度的增强,相应的契约形成的费率也就右移,反之则左移。但是对于不同的风险态度,费率的变动就是无法确定的。这里仅就给出保险契约成立背后费率的合理区间。
三、比例赔付下投保人和保险人溢价模型及合同成立条件
对于上文中保险人溢价模型中,存在假设保险人的赔付是足额的,但是在实际之中这只是特殊情况。一般地,保险人的赔付是按照投保人投保金额和保险价值的比例进行的,即比例赔付。因此,在保险人溢价模型的基础之上,本文将保险人更一般的赔付情况考虑进去。
(一)投保人的风险溢价
假设投保人按照费率 投保,保额为 投保,保额为 , , ,保险价值为 ,保险价值为 , , ,从而保险人的赔付就成了关于投保人损失 ,从而保险人的赔付就成了关于投保人损失 的一个函数: 的一个函数: 。注意到,当保额等于保险价值的时候(即 。注意到,当保额等于保险价值的时候(即 )就是全额赔付。由于损失额与赔付额的不相等,所以投保人此时投保后面临的效用不再像全额投保那样是一个确定的财产价值,而是关于损失变量 )就是全额赔付。由于损失额与赔付额的不相等,所以投保人此时投保后面临的效用不再像全额投保那样是一个确定的财产价值,而是关于损失变量 的期望效用: 的期望效用: 。一方面,投保人投保一定是因为投保所带来的效用要大于不投保的效用。另一方面,对于一定的保险金额,费率越低,投保人缴纳的保费就越少,以此带来的效用就越大。但是从保险人的角度考虑,保险人所收取的纯保费依然要等于他的期望赔付 。一方面,投保人投保一定是因为投保所带来的效用要大于不投保的效用。另一方面,对于一定的保险金额,费率越低,投保人缴纳的保费就越少,以此带来的效用就越大。但是从保险人的角度考虑,保险人所收取的纯保费依然要等于他的期望赔付 ,这是保险人最低的保费要求,如果小于这个值保险人是不会承保的。综合两方面分析并根据Jessen不等式,可以得到: ,这是保险人最低的保费要求,如果小于这个值保险人是不会承保的。综合两方面分析并根据Jessen不等式,可以得到:
 (12) (12)
现在考虑投保人的风险溢价。 2/3 首页 上一页 1 2 3 下一页 尾页 |


