摘要:股票市场中投资者的理性和非理性程度以及相关的生存性,一直是行为金融学研究的热点问题。本文在给出理性投资者和非理性投资者定义的基础上,运用博弈论中一般均衡模型,分析了完全竞争股票市场中理性投资者和非理性投资者之间的生存性关系,在此基础上应该做出怎样的决策,从而可以最大化自己的利益。
论文关键词:布朗运动; 理性投资者;非理性投资者;博弈论;均衡
投资者可以根据经济状况变化的各种可能及其客观概率来决定自己的投资行为,他们惟一的目标就是最大化不确定状况下的期望效用。然而,由于错误的信念,非理性投资者在完全竞争市场中难以长久生存下去,他们在错误的信念下不断地进行交易,使其资产不断损失,并最终导致财富损失殆尽,迫使他们不得不离开股票市场,在股票市场上消亡。所以从长期来看,理性投资者将控制市场上的大部分资产并决定资产的价格。然而,本文借助于2种不同效用函数下一般均衡模型分析后得到,具有错误信念的非理性投资者也将会在股票市场上长期共存。
假定市场是完全竞争的,只有理性投资者和非理性投资者。所有的投资者都是以最大化自己的消费效用为目标的。
一、给出几个定义:
对于市场的不确定性我们可以由标准布朗运动 来描述,它的真实概率空间为 来描述,它的真实概率空间为 ,其中 ,其中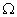 是股票市场的样本空间, 是股票市场的样本空间, 是 是 , , 是概率测度。概率空间 是概率测度。概率空间 是基于某种错误概率信念 是基于某种错误概率信念 之下对股票市场认识的概率空间,称为非理性概率空间。当 之下对股票市场认识的概率空间,称为非理性概率空间。当 和 和 分别相同时,称概率空间 分别相同时,称概率空间 为有限理性概率空间。 为有限理性概率空间。
定义1 依据概率空间 获取并处理信息的投资者我们称为理性投资者。 获取并处理信息的投资者我们称为理性投资者。
定义2 依据概率空间 获取并处理信息的投资者我们称为非理性投资者。 获取并处理信息的投资者我们称为非理性投资者。
定义3 依据概率空间 获取并处理信息的投资者我们就称为有限理性投资者。 获取并处理信息的投资者我们就称为有限理性投资者。
对此,我们可以假定,股票市场上有两种金融资产:风险性金融资产-----股票;无风险性金融资产----零息债券。股票(或债券)在 时刻的价格为 时刻的价格为 所支付的红利为 所支付的红利为 ,并且 ,并且 符合几何布朗运动过程 符合几何布朗运动过程 ,且有: ,且有:
 (1) (1)
其中 为初始红利。 为初始红利。
然而非理性投资者对股票市场的认识是基于错误信念 之下的标准布朗运动 之下的标准布朗运动 ,且有: ,且有:
 (2) (2)
其中 反映非理性投资者的非理性程度, 反映非理性投资者的非理性程度,
所以 。 。
尽管理性投资者与非理性投资者的信念不同,但是我们可以合理地假定对零概率事件或概率为1的事件上二者有一致的认识。依据拉冬---尼科迪母(Radon-Nikodym)定理可知,一定存在一个随机变量函数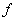 ,使得 ,使得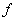 可以反映两类投资的信念间的相对密度函数,不妨设 可以反映两类投资的信念间的相对密度函数,不妨设
关于小学教育的论文  (3) (3)
定义4 (1)若 ,则称在股票市场上只有非理性投资者可以长期存在,而理性投资者不能长期存在。 ,则称在股票市场上只有非理性投资者可以长期存在,而理性投资者不能长期存在。
(2)若  ,则称在股票市场上只有理性投资者可以长期存在,而非理性投资者不能长期存在。 ,则称在股票市场上只有理性投资者可以长期存在,而非理性投资者不能长期存在。
(3)若上述的(1)和(2)都不成立,则称在股票市场上理性投资者与非理性投资者可以长期共同生存。
二、效用函数是指数函数形式分析其生存性
考虑标准边际指数效用函数 ,所以效用函数的形式为: ,所以效用函数的形式为:
 (4) (4)
其中 ,C为某一常数,C的取值可以始终保证此效用函数 ,C为某一常数,C的取值可以始终保证此效用函数 的正值性。由于C的常数性质,只是相当于提高了效用的基础水平,并不影响效用函数的根本性质。为了简化起见,在不影响分析结果的情况下,我们可以采用如下的效用函数形式: 的正值性。由于C的常数性质,只是相当于提高了效用的基础水平,并不影响效用函数的根本性质。为了简化起见,在不影响分析结果的情况下,我们可以采用如下的效用函数形式:  (5) (5)
其中 , , 表示在时间 表示在时间 上的消费。 上的消费。
我们分别以 , , 表示理性投资者和非理性投资者到 表示理性投资者和非理性投资者到 时刻的消费量。从而,非理性投资者的决策问题就是最大化自己利益的如下问题: 时刻的消费量。从而,非理性投资者的决策问题就是最大化自己利益的如下问题:
 (6) (6)
对此理性与非理性两类投资者竞争一种风险证券的市场均衡问题我们就可以利用博弈论 ,建立如下一般均衡模型: ,建立如下一般均衡模型:

  (7) (7)
其中 表示非理性投资者的效用在市场中的权重。 表示非理性投资者的效用在市场中的权重。
对于上述(7)式的一般均衡模型我们利用拉格朗日求极值法,可以得:

其均衡 的条件为: 的条件为:

解得:
 (8) (8)
其中 。 。
根据定义4,并由上述(8)式得到:
  (9) (9)
由于 是标准布朗分布,根据其性质,所以必定存在一个正数 是标准布朗分布,根据其性质,所以必定存在一个正数 ,使得: ,使得:

令
当 ,从而 ,从而 
所以

即在股票市场上只有理性投资者可以长期存在,而非理性投资者不能长期存在。此时,理性投资者就可以一大部分的资金用来购买无风险的债券,一小不部分的资金可以用来投资高风险的股票。
当 ,并且 ,并且 即 即  时,有: 时,有:

所以,

由于 是标准布朗运动过程,所以这是一个对数正态分布 是标准布朗运动过程,所以这是一个对数正态分布 。由此可以断定此情况下,理性投资者与非理性投资者可以在市场上共同长期存在。 。由此可以断定此情况下,理性投资者与非理性投资者可以在市场上共同长期存在。
三、效用函数是对数函数形式分析其生存性
考虑标准边际指数效用函数 ,所以效用函数的形式为: ,所以效用函数的形式为:
 (10) (10)
其中  ,C为某一常数,C的取值可以始终保证效用函数 ,C为某一常数,C的取值可以始终保证效用函数 的正值性。为了简化起见,在不影响分析结果的情况下,我们可以采用如下的效用函数形式: 的正值性。为了简化起见,在不影响分析结果的情况下,我们可以采用如下的效用函数形式: (11) (11)
其中  , , 表示在时间 表示在时间 上的消费。 上的消费。
我们再分别以 , , 表示理性投资者和非理性投资者到 表示理性投资者和非理性投资者到 时刻的消费量。从而,非理性投资者的决策问题就是最大化自己利益的如下问题: 时刻的消费量。从而,非理性投资者的决策问题就是最大化自己利益的如下问题:

(12)
对此理性与非理性两类投资者竞争一种风险证券的市场均衡问题我们利用博弈论可以建立一般均衡模型:

  (13) (13)
同理,对此一般均衡模型利用拉格朗日极值法,得:

其均衡条件为:

解得:
 会计本科毕业论文 (14) 会计本科毕业论文 (14)
其中 。 。
根据定义4,并由上述(14)式得到:

 (15) (15)
由于 是标准布朗分布,所以必定存在 是标准布朗分布,所以必定存在 ,使得: ,使得:

令
当 , , 

所以,

即在股票市场上理性投资者与非理性投资者可以长期共同生存。
当  ,并且 ,并且 即 即  时,有: 时,有:

所以有:

由于 是标准布朗运动过程,所以这是一个对数正态分布。由此可以断定此情况下,理性投资者与非理性投资者可以在市场上共同长期存在。 是标准布朗运动过程,所以这是一个对数正态分布。由此可以断定此情况下,理性投资者与非理性投资者可以在市场上共同长期存在。
所以,对于效用函数是对数形式的,在股票市场上理性投资者和非理性投资者始终可以共同长期存在。
四、结论
股票市场中投资者的理性和非理性程度以及相关的生存性,一直是行为金融学研究的热点问题。本文在给出理性投资者和非理性投资者定义的基础上,对股票市场上两种不同效用函数分别建立了博弈论中一般均衡模型,并研究和分析了完全竞争股票市场中2种不同效用函数下理性投资者和非理性投资者之间的生存性关系。效用函数是指数形式时,理性投资者和非理性投资者可以长期共同存在,也不能够共同长期存在;而效用函数是对数形式时,理性投资者和非理性投资者始终是可以长期共同存在的。
参考文献:
[1]S.M.劳斯.《随机过程》,北京,中国统计出版社,1997.7.
[2]张维迎.《博弈论与信息经济学》,上海,上海人民出版社,1996年版.
[3]杜文意,任晓婷,谭建国. 我国证券市场监管的博弈研究[J].全国商情,2008年6月.
[4]林元烈.《应用随机过程》,北京,清华大学出版社,2002.11. |


