论文摘要:目前,我国大多学者在运用效用函数确定保险费率时,都以投保人全额投保和保险人全额赔付为前提推出保险费率的定价区间。然而,由于各投保人风险态度迥异,不一定总对保险标的全额投保。基于保险定价对保险公司理论研究和实务操作的现实意义,本文首次放松上述假设条件,按照比例投保和比例赔付的方式,通过改进以往投保双方的风险溢价模型,求出保险契约成立的费率区间,并阐述保险费率背后的数理经济学原理。
论文关键词:效用函数,风险规避,风险溢价,比例赔付
一、引言
所谓保险定价,就是保险费率的制定。从世界范围看,定价风险一直都是保险业的重要风险来源。随着我国保险经营的经济金融环境日趋复杂,保险业不断进入新的业务领域,保险公司的定价风险在加大。如果保险业在公司管控、定价能力和监管水平等方面跟不上,就有可能出现新的定价风险。因此,保险定价及其管理是保险监管和理论研究的重要基础工作,进一步贯彻落实与加强保监会对保险费率制定的各项要求,切实营造公平公正、规范有序的保险市场秩序对当前的保险市场发展具有十分重要的现实意义。保险定价是保险实务和理论研究的核心问题之一,它不同于一般商品定价的特殊性在于其对象是对“风险”——未来结果的不确定性。在对不确定性的讨论中,冯·诺依曼的期望效用函数给出了一个比较好的解答。人们对于未来的不确定性,追求的是期望效用的最大化,这样就奠定了保险价格存在的基础。
在期望效用函数引入下,通过对投保人的行为分析,很容易得到禀赋条件下投保人对保费的选择。然而,在随后的分析中逐渐发现,保险费率的确定不仅仅是依赖于投保人的选择,实际上保险人作为承担保险的一方,对保险费率也有着重要的决定权。
周宏(1994),运用效用理论分析了保险行为中的两个变量,投保人和保险人双方的风险态度,通过影响保险双方所能接受的风险概率范围来影响保险行为的内在机理。夏龙梅等人(2002),通过建立保险的博弈模型,深入地探讨了保险价格发生变化时对投保人和保险人的比较静态分析,得到了保险的需求和供给水平随价格变化的规律。荣喜民等人(2003)利用随机微分方程建立了以承保风险为控制变量的保险投资定价模型,并通过分析给出了由投资决定的保险价格公式。由投资来发现保险价格,为保险人进行保险价格调整提供了依据,并给出了一个保险价格的投资定价流程。张勇(2004)也指出,厘订保险费率的决策是保险公司管理者需主要关注的问题之一,并从保险经济学、从合理决策的角度出发讨论保险定价问题。魏世勇等人(2008)在文献中先结合消费者效用函数,从理论上确定保险人所能接受的最低价格和投保人所愿意支付的最高价格,用一个数学模型的形式对保险定价问题做出了定量分析,从经济学的效用理论的角度来分析投保人和保险人在既定的市场环境中如何确定保险价格的,以此确定保险价格的取值范围。
但从大多数文献来看,在应用效用函数来确定保险定价和使投保人效用最大化的模型背后都运用了这样一个假设:保险人全额赔付和投保人对自己的风险概率已知。在该假设条件下通过效用理论可以求得投保人的最优解,也就是全额投保,并且此时保险人的费率与投保人的风险概率一致。然而,投保人实际上对自己所面对的风险发生概率是无法定量估计的。因此在上面提到的有约束条件下求得投保人效用最大的解的实际应用价值是不大的。现在放松这两个假设条件,分析比较投保人和保险人各自能够接受的保费的上下限,这样就能对保险费率给出一个合理的区间,而不是一个确定的值。
本文首先在投保人全额投保与保险人全额赔付的假设下分析保险定价模型。随后,放松上述假设,推出保险费率定价的一般区间,并通过这一费率区间,阐述保险价格背后的数理经济学原理。
二、全额赔付下投保人和保险人溢价模型及合同成立条件
如果消费者是一个厌恶风险并且追求期望效用最大化的人,同时他可以为潜在的损失购买公平保险,那么他的最优选择就是完全保险。下面分别从投保人以及保险人的角度来探讨此问题。
(一)投保人的风险溢价
在自己的财产面临未来不确定性的时候,通常人们会选择保险这种风险规避的方法来保证自己未来财产的安全。假设投保人都是厌恶风险的,并采用效用函数来表示财产给人们带来的效用。但此时在考虑未来不确定性条件下的效用时,采用冯·诺依曼效用函数来刻画。
假设投保人初始财产为 ,未来风险损失为随机变量 ,未来风险损失为随机变量 ,且 ,且 服从某一分布, 服从某一分布,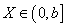 , , 表示保险价值,且 表示保险价值,且 。假设 。假设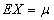 , , , , 表示保险金额, 表示保险金额, 是保险费率。效用函数是理性人对偏好的度量,在这里假设投保人和保险人都具有良性偏好和风险规避的特征,满足偏好的单调性、凸性,有: 是保险费率。效用函数是理性人对偏好的度量,在这里假设投保人和保险人都具有良性偏好和风险规避的特征,满足偏好的单调性、凸性,有:
 , ,
我们用横坐标表示投保人未来财产,纵坐标表示投保人效用,那么投保人的效用函数图像如图1所示:
 
图1投保人的效用分析
当投保人没有投保时,他的期望效用是 。现在考虑如果全额投保,那么投保人损失 。现在考虑如果全额投保,那么投保人损失 ,必然能从保险人那里获得赔付 ,必然能从保险人那里获得赔付 ,因此投保人未来财产是确定的,即 ,因此投保人未来财产是确定的,即 。投保人之所以选择投保,是因为投保后带给投保人的效用将会大于其不投保时的效用,即 。投保人之所以选择投保,是因为投保后带给投保人的效用将会大于其不投保时的效用,即 ,并且随着全额保费的降低,投保人的效用将会增大。但是全额保费会降低至什么程度呢?实际上,保险人收入的最低纯保费是与他赔付的期望值相等的,即 ,并且随着全额保费的降低,投保人的效用将会增大。但是全额保费会降低至什么程度呢?实际上,保险人收入的最低纯保费是与他赔付的期望值相等的,即 。因此,全额保费 。因此,全额保费 最低不会小于 最低不会小于 ,所以有 ,所以有 。 。 1/3 1 2 3 下一页 尾页 |


