| 学年第一学期高三年级七校期中联考卷第21题)
已知向量 , , ,满足 ,满足 (其中 (其中 ). ).
(1)求函数 的解析式; 的解析式;
(2)若 ,求函数 ,求函数 在 在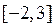 上的最大值与最小值; 上的最大值与最小值;
(3)对任意的 ,是否存在实数 ,是否存在实数 使得 使得 恒成立?若存在,求出 恒成立?若存在,求出 的取值范围;若不存在,说明理由. 的取值范围;若不存在,说明理由.
对于这道题的第三小题
参考答案是这样给出的.
(3)解:对任意的 , , 恒成立,即函数 恒成立,即函数 在 在 上的最大值小于5.而 上的最大值小于5.而
①当 时, 时, ,函数 ,函数 在 在 上单调递增, 上单调递增, ,所以得 ,所以得 ; ;
②当 时,函数 时,函数 在 在 递增, 递增, 递减, 递减, 递减, 递减, 递增,所以 递增,所以 ,解得 ,解得 ; ;
③当 时,函数 时,函数 在 在 上单调递减, 上单调递减, ,所以 ,所以 . .
综上所述, 取值范围为 取值范围为 . .
对于这个解法学生分类讨论难度较大,且②中的3是怎么得来的呢?其实我们需要先对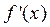 的正负先进行一个判断,得到两个极值点.再对该极值点是否在 的正负先进行一个判断,得到两个极值点.再对该极值点是否在 中进行讨论,得出 中进行讨论,得出 在3这一点需要进行分类讨论.但是,我们能用上面提到的恒成立的解题方法换个角度再来解决这个题目吗?我们能否把平时积累的解题方法在解决新题时使用,并加快解题速度,优化解题方法呢?在这道题的题后反思中,我们能不能减少讨论,更快寻求 在3这一点需要进行分类讨论.但是,我们能用上面提到的恒成立的解题方法换个角度再来解决这个题目吗?我们能否把平时积累的解题方法在解决新题时使用,并加快解题速度,优化解题方法呢?在这道题的题后反思中,我们能不能减少讨论,更快寻求 的取值范围呢?对此,我们尝试对不等式先进行变量分离,再通过最值求解不等式恒成立问题. 的取值范围呢?对此,我们尝试对不等式先进行变量分离,再通过最值求解不等式恒成立问题.
【解法优化】:对于 在 在 上恒成立,即求 上恒成立,即求 恒成立. 恒成立.
①当 时,不等式恒成立. 时,不等式恒成立.
②当 时,即求 时,即求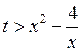 恒成立,只需求 恒成立,只需求 大于 大于 在 在 上的最大值,而 上的最大值,而 是一个在该区间内单调递增的函数.所以 是一个在该区间内单调递增的函数.所以 ,所以 ,所以
③当 时,即求 时,即求 恒成立,只需求 恒成立,只需求 小于 小于 在 在 上的最小值,而此时 上的最小值,而此时 ,则 ,则 是一个在该区间内单调递减的函数.所以 是一个在该区间内单调递减的函数.所以 ,所以 ,所以 . .
综上所述, 取值范围为 取值范围为 . .
上述两种方法从两个不同的角度解答了这个题目.但是在你脑海里是否能和平时的练习建立联系,能否通过这两个题的分析与反思丰富你的知识网络.我们教师需要做的便是在平时的课堂中,试题讲评的过程中,不断引导学生进行题后反思,只有这样不断的产生解题思路的关联,才能逐步的提高自己的解题水平.
在我们平时的教学过程中,只要我们留心,就能发现很多相类似的题型以及解题思路与方法.我们不要以一种“炒冷饭”的形式,机械化地“传输”给学生.而是通过认真、仔细的题后反思与归纳总结,使学生的解题思路更加融会贯通.在反思过程中,可以引导学生不断地总结解决问题的方法、技能以及经验教训.在“解题反思”的教学中,教师上课不再是“一言堂”,而常常让学生参与,让学生发表见解,因而学生的主体性得到很好的体现.教师在聆听中,经常得到启迪,诱发教学反思,进而不断改进教法,增强教学的有效性.同时引导学生真正领悟数学的思想和方法,优化认知结构,提高思维能力,从而更大地发挥和提高学生的智能和潜能.从而培养出一支真正会解题的学生队伍. 2/2 首页 上一页 1 2 |


