摘要:在数学教学中,加强“解题反思”的研究,有利于教师改进教学方法,增强教学的有效性,有利于学生在学习中进行自我评价和自我调节,学会学习,从而提高学习质量.本文从优化解题方法,系统归纳题型,构建知识网络等方面介绍了如何在高三复习中引导学生进行解题反思.使学生解题思路分析更加清晰,新旧题目更加连贯,从而使解题效率得以提高.
论文关键词:解题,反思,系统归纳
“解题反思”是数学学习的需要,也是新课标的要求.反思是指对自身的思维过程、思维结果进行再认识和检验的过程,是认知过程中强化自我意识、进行自我监控、自我调节的主要形式.荷兰著名数学教育家弗赖登塔尔指出,“反思是数学思维活动的核心和动力”.
联系高三数学复习备考的实际,无论是在第一轮知识方法系统的重新构建,还是在第二轮的专题强化训练中,解题教学无疑占据着“半壁江山”.各种训练题、模拟题层出不穷,铺天盖地,甚至成为不少学生每天殚精竭虑、疲于奔命的主流生活,也成为一些教师手中提升学生应考能力的法宝.但是“题海无边,何处是岸?”,学生“题海挣扎”的结果又如何?面对一些学生一次次在同一个坎上跌倒,一次次在同一个“陷阱”里失足……难道不能引起教师的反思、深思?
下面我们从“试题解法优化”这个角度阐述如何在高三复习中引导学生进行解题反思.
一、认真审题,针对不同的题型采取不同的解题方法
例1.(2007年天津文科卷第10题)设 是定义在 是定义在 上的奇函数,且当 上的奇函数,且当 时, 时, ,若对任意的 ,若对任意的 ,不等式 ,不等式 恒成立,则实数 恒成立,则实数 的取值范围是() 的取值范围是()
A.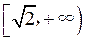 B. B. C. C. D. D.
【解法一】:作为一个压轴的选择题,我们该采取怎样的解题方法呢?首先当然针对选择题的特点,通过对四个选项的观察,能否对A,B,C,D四个选项中的某个特殊值进行代入验证.对于A,B两个选项,我们选择 首先进行代入,则 首先进行代入,则 ,代入得 ,代入得 恒成立,所以排除了B选项.对于A,C选项,我们令 恒成立,所以排除了B选项.对于A,C选项,我们令 ,则 ,则 ,不等式 ,不等式 不恒成立,所以排除C选项.对于A,D选项,我们选择 不恒成立,所以排除C选项.对于A,D选项,我们选择 代入,因为 代入,因为 是定义在 是定义在 上的奇函数,则当 上的奇函数,则当 时 时 .同样不等式不恒成立.故答案选A. .同样不等式不恒成立.故答案选A.
作为考试,我们通过上述方法得到了正确得答案,那么在考试之后呢?我们反思:
(1)如果该题是个填空题,到底该如何解答?
(2)答案中的 又是怎么出来的呢? 又是怎么出来的呢?
该题的难点在于仅知道 时的函数解析式,通过奇函数得到 时的函数解析式,通过奇函数得到 的函数解析式.但是当 的函数解析式.但是当 时我们没有办法确定此时 时我们没有办法确定此时 的正负符号.有此产生以下解题方法二,对 的正负符号.有此产生以下解题方法二,对 的范围通过 的范围通过 进行分类讨论. 进行分类讨论.
【解法二】:此题是一个不等式恒成立问题,结合函数得奇偶性,我们得到当 时, 时, ;当 ;当 时, 时, . .
讨论:①当 时, 时, ,所以 ,所以 ,即 ,即 恒成立,在 恒成立,在 时,令 时,令 ,只要 ,只要 恒成立即可.解得 恒成立即可.解得 . .
②当 时, 时, ,所以有 ,所以有 ,即 ,即 ,在 ,在 时,令 时,令 只要 只要 恒成立即可.而 恒成立即可.而 恒小于零,故无解. 恒小于零,故无解.
③当 且 且 时,因为 时,因为 ,又有如下讨论: ,又有如下讨论:
(Ⅰ)当 时,易知 时,易知 由该奇函数函数得单调性可知 由该奇函数函数得单调性可知 ,又因为 ,又因为 ,所以 ,所以 ,得到 ,得到 与题条件矛盾,故无解. 与题条件矛盾,故无解.
(Ⅱ)当 时, 时, ,则 ,则 即上述②得讨论,故无解. 即上述②得讨论,故无解.
综上所述, 得取值范围为 得取值范围为 . .
二、审视解题过程,思考解题方法是否最佳
解法一比较适合选择题的使用,但是就像刚才提到的,我们并没有真正计算出 的取值范围.解法二详细地求出了变量 的取值范围.解法二详细地求出了变量 的取值范围,但是作为一个选择题,这种解题方法太过复杂,且分类讨论难度过大.因此,解法二不适合考试时求解该题.因此,我们能否问问自己,这题就只有这些方法吗? 的取值范围,但是作为一个选择题,这种解题方法太过复杂,且分类讨论难度过大.因此,解法二不适合考试时求解该题.因此,我们能否问问自己,这题就只有这些方法吗?
进一步引导学生思考:可不可以换个角度另辟佳径?在上述解题过程中提到一个重要得题目信息,就是该函数得单调性.由题可得 在R上是单调递增函数,那么能否利用函数的单调性来解决问题呢?若是简单的不等式 在R上是单调递增函数,那么能否利用函数的单调性来解决问题呢?若是简单的不等式 恒成立,则可由函数单调递增的性质得 恒成立,则可由函数单调递增的性质得 ,即得 ,即得 .这种解题思路对解决这个高考题能有什么帮助呢?我们怎么处理这道题中多出来得系数2呢?系数2能否去掉呢? .这种解题思路对解决这个高考题能有什么帮助呢?我们怎么处理这道题中多出来得系数2呢?系数2能否去掉呢?
【解法三】:我们发现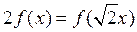 ,那么不等式 ,那么不等式 恒成立,即 恒成立,即 恒成立,只要求 恒成立,只要求 恒成立.再转化为恒成立问题的一般解法 恒成立.再转化为恒成立问题的一般解法 .即求 .即求 这个一次函数在 这个一次函数在 上的最大值 上的最大值 .得到 .得到 ,即 ,即 ,解得 ,解得 . .
到此,上述的一,三两种方法都能很好的解决这样一个高考选择题,通过这样的题后反思,使学生更能感受到数学的魅力,以及体会解题成功的那种成就感.
三、系统归纳数学方法,探求一般规律
即使数学题灵活多边,方法千变万化,然而也并非是神秘莫测,和解决千千万万的矛盾一样,是有一定有规律可循的.必须系统总结,反复多练,才能以不变应万变.
如上例中的恒成立问题.我们在复习过程中曾做到过这样的一个试题.
例2.已知定义域为 的函数 的函数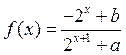 是奇函数.(1)求 是奇函数.(1)求 的值;(2)若对任意的 的值;(2)若对任意的 ,不等式 ,不等式 恒成立,求 恒成立,求 的取值范围. 的取值范围.
对于该题(2)的解题思路,和例1是一样的.那么同学们在题后系统归纳解题方法时能否将两道题进行归类重组呢?不等式   ,再利用(1)可以求得该函数是奇函数,且在R上单调递减.则上式即为 ,再利用(1)可以求得该函数是奇函数,且在R上单调递减.则上式即为 ,最后即求 ,最后即求 恒成立.对于此类恒成立问题,仍然可以用分离变量的方法得到 恒成立.对于此类恒成立问题,仍然可以用分离变量的方法得到 ,即 ,即 小于 小于 在 在 上的最小值,解得 上的最小值,解得 .同样都是利用到函数本身所具有的单调性,不通过函数解析式的代换,而是直接通过自变量的大小的比较来直接求解.大大加快了解题速度,增加了解题的灵活性. .同样都是利用到函数本身所具有的单调性,不通过函数解析式的代换,而是直接通过自变量的大小的比较来直接求解.大大加快了解题速度,增加了解题的灵活性.
四、不断积累解题经验,提高解题效率
解题方法、思路的积累,最后还是在于能否融会贯通解决新题,在平时的考试中,能否唤醒你解题的思路与灵感.在今年的期中考联考卷中出现了这样的一个题.
例3.(浙江省杭州地区2009-2010
1/2 1 2 下一页 尾页 |


