焦点弦公式及其应用
论文关键词:焦点弦公式,应用
在近年来的高考数学试题中,经常出现圆锥曲线焦点弦问题.用常规方法解决这类问题时,由于解题过程复杂,运算量较大,所以很容易出现差错.
为了准确而迅速地解决圆锥曲线焦点弦问题.我们可以利用下面介绍的焦点弦公式.
 设圆锥曲线的离心率为 设圆锥曲线的离心率为 ,焦准距为 ,焦准距为 ,过焦点的弦AB与主轴(即椭圆长轴、双曲线实轴、抛物线对称轴)的夹角为θ,则可以推导出弦AB的长度公式 ,过焦点的弦AB与主轴(即椭圆长轴、双曲线实轴、抛物线对称轴)的夹角为θ,则可以推导出弦AB的长度公式  ,简称焦点弦公式.特别当离心率 ,简称焦点弦公式.特别当离心率 时,焦点弦公式还可以化简. 时,焦点弦公式还可以化简.
1、当 时,圆锥曲线为椭圆, 时,圆锥曲线为椭圆,  ; ;
2、当 时,圆锥曲线为抛物线, 时,圆锥曲线为抛物线,  . .
下面对焦点弦公式进行证明.
证法一如图1,设椭圆C: 焦点为 焦点为 ,过焦点F的弦AB的倾斜角为 ,过焦点F的弦AB的倾斜角为 ,当 ,当 时,弦AB在直线 L: 时,弦AB在直线 L: 上.由直线L和椭圆C的方程可得 上.由直线L和椭圆C的方程可得
 . .
设点A、B的坐标分为 和 和 ,则 ,则 .由焦半径公式得弦AB的长度为 .由焦半径公式得弦AB的长度为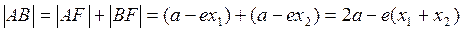       
∵焦准距为 ,∴ ,∴ .当 .当 时,公式也成立. 时,公式也成立.
对于双曲线和抛物线用同样的方法可以证明.
证法二设圆锥曲线的离心率为 ,焦准距为 ,焦准距为 ,则极坐标方程为 ,则极坐标方程为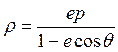 ,过焦点 ,过焦点 的弦AB与x轴的夹角为θ.当 的弦AB与x轴的夹角为θ.当 时,如图2.∵ 时,如图2.∵ , , . .
∴
 .即 .即 . .
当 时,同理可以推得 时,同理可以推得 . .
利用焦点弦公式,可以巧妙地解决与圆锥曲线焦点弦有关的各种问题.现在分别举例如下.
一、在椭圆中的应用
例1 (2008年高考安徽卷文科22题)
已知椭圆 ,其相应于焦点F(2,0)的准线方程为x=4. ,其相应于焦点F(2,0)的准线方程为x=4.
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知过点F1(-2,0)倾斜角为 的直线交椭圆C于A,B两点.,求证: 的直线交椭圆C于A,B两点.,求证:
(Ⅲ)过点F1(-2,0)作两条互相垂直的直线分别交椭圆C于点A、B和D、E,求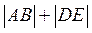 的最小值. 的最小值.
解:(Ⅰ)由已知得 ,又 ,又 ,所以 ,所以 . .
故所求椭圆C的方程为 . .
(Ⅱ)因为直线AB倾斜角为 , ,  , , , , , ,  。 。
由焦点弦 ,可得 ,可得 = = 得证. 得证.
(Ⅲ)因为直线AB倾斜角为 ,则DE与 ,则DE与 轴的夹角可表示为 轴的夹角可表示为 。因而 。因而
 , , , ,
  
 。 。
1/2 1 2 下一页 尾页 |


