论文摘要:受曹广福教授和Josepha.Cima教授的文章的启发,研究多圆盘上Bergman空间中具有无界符号的Toeplitz算子的有界性、紧性。
论文关键词:算子,无界函数,空间
一、引言
记D是复平面内的单位圆盘,T是单位圆周,对确定的正整数n, 分别是n个D,T的笛卡尔积,不难证明 分别是n个D,T的笛卡尔积,不难证明 是 是  的Shilov边界[8,9], 的Shilov边界[8,9], 表示 表示 的拓扑边界,本文所涉及的边界问题只考虑Shilov边界。 的拓扑边界,本文所涉及的边界问题只考虑Shilov边界。 表示Bergman空间,在 表示Bergman空间,在 上关于正规化的Lebesgue面积测度dA是平方可积的,且在 上关于正规化的Lebesgue面积测度dA是平方可积的,且在 上是解析的函数空间。对 上是解析的函数空间。对 ,用 ,用 表示 表示 上以f为符号的Toeplitz算子,其定义如下: 上以f为符号的Toeplitz算子,其定义如下: 其中P表示 其中P表示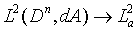 上的正交投影,此算子是稠密定义的。在[1]中,曹广福教授在单位球上构造了一类无界函数,使以之为符号的Toeplitz算子是紧的,并且,构造了在单位球的每个边界点的任意领域上的无界函数,以其为符号的Toeplitz算子是trace类算子。在[2]中Axler刻画了D上的有界符号诱导出Toeplitz算子在Bergman空间上何时是紧的。在[3]中,Grudsky和Vasilevski证明了以径向函数为符号的Toeplitz算子在 上的正交投影,此算子是稠密定义的。在[1]中,曹广福教授在单位球上构造了一类无界函数,使以之为符号的Toeplitz算子是紧的,并且,构造了在单位球的每个边界点的任意领域上的无界函数,以其为符号的Toeplitz算子是trace类算子。在[2]中Axler刻画了D上的有界符号诱导出Toeplitz算子在Bergman空间上何时是紧的。在[3]中,Grudsky和Vasilevski证明了以径向函数为符号的Toeplitz算子在 上是有界(或紧)的,当且仅当序列 上是有界(或紧)的,当且仅当序列 。在[5]中Josepha.Cima研究了在单位圆盘上Bergman空间 。在[5]中Josepha.Cima研究了在单位圆盘上Bergman空间 中以无界函数为符号的Toeplitz算子的紧性问题。 中以无界函数为符号的Toeplitz算子的紧性问题。
二、有界性
本部分在多圆盘 上构造满足一定增长条件的无界函数.首先在 上构造满足一定增长条件的无界函数.首先在 的子域上构造特定的类型使得这些无界函数在 的子域上构造特定的类型使得这些无界函数在 的正测度集上"膨胀",但其相应的Toeplitz算子仍是有界的,或紧的。设“锥点”域 的正测度集上"膨胀",但其相应的Toeplitz算子仍是有界的,或紧的。设“锥点”域 其中m,b的值视研究的具体情况而定。对 其中m,b的值视研究的具体情况而定。对 上的任意点 上的任意点 ,设 ,设 是 是 在 在 旋转,再“膨胀” 旋转,再“膨胀” ,使得对某个 ,使得对某个 ,满足 ,满足 且 且 .设序列 .设序列 恰好是某个Cantor集的顶点。首先在[0,1]区间构造Cantor集,去掉中间长度为 恰好是某个Cantor集的顶点。首先在[0,1]区间构造Cantor集,去掉中间长度为 的部分 的部分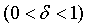 ,在剩下的两个不相交的区间中再分别去掉长度为 ,在剩下的两个不相交的区间中再分别去掉长度为 的中间部分,依次重复这个过程..此过程在[0,1]上产生一个紧的正测度集A,对A作n个笛卡尔积,设 的中间部分,依次重复这个过程..此过程在[0,1]上产生一个紧的正测度集A,对A作n个笛卡尔积,设 ,通过函数 ,通过函数 ,把M映射到 ,把M映射到 ,且 ,且 是顶点的像.因此,每个 是顶点的像.因此,每个 在 在 达到 达到 ,且可选择 ,且可选择 使得它们是不相交的。设 使得它们是不相交的。设 ,考虑一个可测函数H(z)满足 ,考虑一个可测函数H(z)满足 其中0,使得对每个球 其中0,使得对每个球 (以 (以 为球心,r为半径),及任意r值,有 为球心,r为半径),及任意r值,有
 。定义 。定义  是 是 的特征函数,显然h在每个 的特征函数,显然h在每个 点趋向无穷大.又因为 点趋向无穷大.又因为 中的Cantor集的其它点是顶点 中的Cantor集的其它点是顶点 的极限点,所以h在 的极限点,所以h在 的Cantor集的其它点也趋向无穷大.因此,得出结论:在 的Cantor集的其它点也趋向无穷大.因此,得出结论:在 的正测集上,h为无穷大.易证当 的正测集上,h为无穷大.易证当 时,选择适当的b与 时,选择适当的b与 ,可使 ,可使 下面讨论Toeplitz算子 下面讨论Toeplitz算子 的有界性。 的有界性。
定理1.1:设H(z)是 上具有增长速度为 上具有增长速度为 的可测函数,其中0,对 的可测函数,其中0,对 上的任意Cantor集,其顶点 上的任意Cantor集,其顶点 ,存在 ,存在 与不相交集 与不相交集 , , 为集合 为集合
 在 在 旋转而得,且 旋转而得,且 有限,使得若 有限,使得若 ,则符号 ,则符号 诱导 诱导 上的一个有界Toeplitz算子。特别地,当取b=2c+5, 上的一个有界Toeplitz算子。特别地,当取b=2c+5, 时,结论成立. 时,结论成立.
证明:对 , ,
对每个i,
  
若对某一满足b-2c-3>0的常数c,则

取b=2c+5, 上式级数收敛,所以 上式级数收敛,所以 在 在 上有界。.因此,即使符号在 上有界。.因此,即使符号在 的正测度集上趋于无穷,仍可以得到有界的Toeplitz算子。 的正测度集上趋于无穷,仍可以得到有界的Toeplitz算子。
三、紧性
定理1.2:设h与 如定理1.1中所设,则选取合适的b与 如定理1.1中所设,则选取合适的b与 值时,可使 值时,可使 为 为 上的紧算子。 上的紧算子。
证明:选取序列 满足 满足 且 且 在 在 的紧子集上一致收敛到0,我们将证明,当 的紧子集上一致收敛到0,我们将证明,当 时, 时, 。再选取序列 。再选取序列 使得 使得 设 设 ,选定J,则可找到正整数N使得对任意 ,选定J,则可找到正整数N使得对任意 , , 且对 且对 ,有 ,有 .考察 .考察   
现估算 与 与 ,对任意n>N, ,对任意n>N,

对 ,运用Cachy-Schwarz不等式,则 ,运用Cachy-Schwarz不等式,则

若取b=2c+4,则由已知假设得 右边的级数收敛, 右边的级数收敛, 的和小于 的和小于 的常数倍。 的常数倍。
所以,当 时, 时, 故 故 是紧的。 是紧的。
参考文献
1 Cao Guangfu.\ Toeplitz operators with unbounded symbols of several complex variables,Math.Anal.Appl[J].2008,339:1277-1285
2 S.AXLER,D.ZHENG. Compact operators via the Berezin transform,Indianauniv.Math.[J].1998,47:387-400
3 S.GRUDSKY,N.VASILEVSKI.Bergman-Toeplitz operators:Radial compact influence,Integral Equations operator Theory [J].2001,40:16-33
4 J.Miao,D.Zheng.Compact operators on Bergman Spaces,Integral Equations operatorTheory [J].2004,48:61-79
5 JOSEPHA.CIMA,ZELJKO CUCKOVIC,Compact Toeplitz Operators with unbounded symbols,OperatorTheory[J].2005,53:(2),431-440
6 WALTER RUDIN.Function theory in polydiscs,W.A.BenjaminInc.New York-Amsterdan[M].1969
7 Bottema,Reinie Erne.Topics in Elementary Geometry,Springer New York[M].2008,1-6
8 Eberhard Kaniuth,A course in commutative Banach Algebras,Springer New York [M].2009
9 李炳仁。Banach代数,科学出版社[M].1992
|


