一道容易出错的二重积分计算题_定积分

论文导读:：通过对一道二重积分题的错误解法剖析，发现学生知识掌握的薄弱环节，从而引起数学教学上的足够重视，并着重介绍了相应的正确解答．
论文关键词：二重积分，定积分，极坐标替换
 

对于积分区域D的形式，其边界曲线由极坐标方程表示比较方便时，我们一般考虑用极坐标变换来计算二重积分的值，其变换过程为：

令，再将积分区域D用极坐标方法表示之，继而用公式: 转换之.

通常地,当积分区域为中心在坐标轴上的圆形或部分圆形域,或是中心在坐标原点的环形或部分环形域,以及被积函数以、、、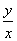为中间变量时,用以上方法计算二重积分是比较行之有效.比较常见的例型有教材^[1]中的例4至例7.

本人在二重积分教学过程中，曾布置过这样一道作业题．

计算二重积分

从学生所交来的作业答案中，竟发现相当多的学生其解答犯有同样的错误,不妨罗列错误解法如下:

解：作极坐标替换，则在极坐标系中，闭区域D可表示为：

于是，

由奇函数在对称区间上定积分的性质，可知：

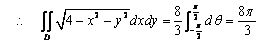
究其原因，一方面，学生对高中的一个根式的性质：，不够重视，平时经常出现类似的错误：．这也是教材在不定积分的三角替换中，没有作进一步的强调所致定积分，如教材中的例题以及后面的小结,都习惯性的只介绍一种三角代换式，忽视了替换中的条件，如等等，当然学生对这样的书写也习惯成自然了．另一方面，诸如对定积分:

，

此类的题型缺乏足够的练习，使得对分段函数的定积分一筹莫展．

本题的正确解法和答案应该是：

解法一：作极坐标替换，则积分区域可表示为：

而对于定积分来说，只要作变量替换，令，则：

解法二：根据二重积分的几何意义，以及球面图形关于坐标轴的对称性，有

作极坐标替换，则积分区域D₁可表示为：

通过本题的讲解和错误修正，笔者认为平时要对不定积分的三角替换、对对称区间的定积分以及绝对值函数的定积分的教学要引起足够重视，计算时要多注说明这些比较容易出错的地方，举一反三，加强该类题型的练习，例如布置一些如下二重积分的计算题型:

⑴. ,其中

⑵. ,其中

总之,计算被积函数带绝对值号的二重积分,要正确去掉被积函数的绝对值号是个关健,注意被积函数在各子区域上的符号,根据积分区域的可加性质才能正确计算.

参考文献［1］桂德怀．高等应用数学(第二册)[M]．苏州：苏州大学出版社，2007．11：80-81.
[2］张国昌．高等数学(第一册)[M]．苏州：苏州大学出版社，2003．8：137-138.
［3］华东师范大学数学系．数学分析（第三版）[M]．北京：高等教育出版社，2001.