摘要:本文在《数学分析》(华东师大版)所叙述的第一、第二积分中值定理和前人对积分中值定理所作的改进的基础上,进一步把定理中的条件进行加强,从而得到一个更精细的定理,并分别从四个方面阐述了积分中值定理的应用。
论文关键词:积分中值定理,函数,连续,单调,区间
中占有重要的地位。
一、 积分中值定理的叙述
定理 :(推广的积分第一中值定理) :(推广的积分第一中值定理)
若函数 与 与 在闭区间 在闭区间 上连续,且 上连续,且 在 在 上不变号,则在 上不变号,则在 上至少存在一点 上至少存在一点 ,使 ,使 。特别地,当g(x)=1时有 。特别地,当g(x)=1时有

定理 :(积分第二中值定理) :(积分第二中值定理)
若函数 在在区间 在在区间 非负单调递减, 非负单调递减, 为可积函数,则存在 为可积函数,则存在  。 。
定理 :若在 :若在 上 上  且单调递增, 且单调递增, 为可积函数, 则存在 为可积函数, 则存在  . .
定理 (推论):若在 (推论):若在 上 上 为单调函数, 为单调函数, 为可积函数,则存在 为可积函数,则存在  。 。
二、 积分中值定理的改进
 将第一中值定理进行改进和加强得到: 将第一中值定理进行改进和加强得到:
定理 :若函数 :若函数 在闭区间 在闭区间 上连续, 上连续, 在 在 上连续且不变号,则在 上连续且不变号,则在 内至少存在一点 内至少存在一点 ,使 ,使 。特别地,当 。特别地,当 =1时有, =1时有,
现在我们在此基础上将定理5中的条件进行加强,从而得到:
定理6:若函数 在闭区间 在闭区间 上严格单调且连续,而 上严格单调且连续,而 在 在 上可积不变号,则在 上可积不变号,则在 内存在唯一一点 内存在唯一一点 ,使 ,使 。特别地,当 。特别地,当 =1时有 =1时有
证明:在区间 中作映射T: 中作映射T: = = + + ,不妨设 ,不妨设 严格单调递增(严格单调递减的情况可类似证明),则 严格单调递增(严格单调递减的情况可类似证明),则    < <  < < ,那么 ,那么 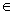 C C ,从而T是 ,从而T是 到自身的映 到自身的映 。又对于 。又对于 ,有: ,有:

因为 在 在 上严格单调递增,所以 上严格单调递增,所以 ,故必存在一个数 ,故必存在一个数 ,使得 ,使得 成立。因此有: 成立。因此有:
 = =  , ,
从而T是 到自身的压缩映像,由Banach不动点原 到自身的压缩映像,由Banach不动点原 ,存在唯一一点 ,存在唯一一点  ,即 ,即
 
从而得 ,定理得证。 ,定理得证。
三、 积分中值定理的应用
1. 在具有某些性质的点的存在问题中的应用
在积分学的学习过程中,有关定积分具有某些性质的点的存在问题的论证是一个难点。一般,我们应仔细观察被积函数所具有的性质,注意利用微分中值定理、积分中值定理等途径来证明有关问题。
例1 若函数 在闭区间 在闭区间 上连续,且 上连续,且 ,证明: ,证明:
在 内至少存在两点 内至少存在两点 。 。
在 中已用Rolle定理给出了一个证明,而本文将利用积分中值定理来证明。 中已用Rolle定理给出了一个证明,而本文将利用积分中值定理来证明。
分析:很明显 =0在闭区间 =0在闭区间 上至少存在一个根,那么我们采用反证法,即证 上至少存在一个根,那么我们采用反证法,即证 =0在 =0在 上不可能只存在唯一的一个根。利用积分中值定理推出矛盾,从而证明命题。 上不可能只存在唯一的一个根。利用积分中值定理推出矛盾,从而证明命题。
证明一: 由 由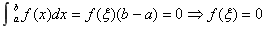 ,即 ,即 =0至少存在一个根。 =0至少存在一个根。
假设在 内 内 =0只有一个根,则由 =0只有一个根,则由 有: 有:
 (1) (1)
因为 与 与 在 在 及 及 连续,且由假设知 连续,且由假设知 在 在 及 及 上不变号。 上不变号。
由定理5得:存在 使得 使得

而 ,于是我们得到 ,于是我们得到 ,这与 ,这与 矛盾。即证在 矛盾。即证在 内至少存在两点 内至少存在两点 。 。
证明二:假设在 内 内 =0只有一个根 =0只有一个根 ,由 ,由 知f(x)在 知f(x)在 内异号。设在 内异号。设在 ,而 ,而 = = 为单调递增函数,所以 为单调递增函数,所以
 这与 这与 矛盾。 矛盾。
例2 设函数 二次可微,且 二次可微,且 严格单调,证明:在 严格单调,证明:在 内存在唯一的一点 内存在唯一的一点 ,使得 ,使得 。 。
在 中有一个类似的例题,联想到定理6,本文的将其中的条件作减弱,将“ 中有一个类似的例题,联想到定理6,本文的将其中的条件作减弱,将“ 具有二阶连续导数”改为“ 具有二阶连续导数”改为“ 二次可微”,然后利用定理6给予证明。 二次可微”,然后利用定理6给予证明。
分析:由题目的条件和结论,我们首先想到将 在 在 = = 处用Taylor公式展开,然后对展开式的两边在区间 处用Taylor公式展开,然后对展开式的两边在区间 上同时积分,然后利用积分中值定理和定理6推出结论。 上同时积分,然后利用积分中值定理和定理6推出结论。
证明:令 = = , , 在 在 = = 处用Taylor公式展开得: 处用Taylor公式展开得:
 ,其中 ,其中 介于 介于 与 与 之间。 之间。
即  (2) (2)
对(2)式两边在区间 上同时积分得 上同时积分得
 (3) (3)
其中 。而|ke 。而|ke
1/3 1 2 3 下一页 尾页 |


