摘要:线性极值定理问题即为求函数的极大值和极小值问题:它不仅是中学数学竞赛中的重要课题,而且也是自然科学、工程技术、国民经济以及生活实践中的常见数学问题.本文着重对任意多个因子的积的极大定理问题,任意多项和的极小定理问题及极大极小定理问题的互逆性的有关定理进行了推广,并举例说明了其简单应用.
论文关键词:线性极值定理,推广,应用
文献[1]给出了任意多个因子的积的极大问题,任意多项和的极小问题及极大极小问题的互逆性的有关定理及应用.本文在此基础上,从有限多个未知数推广到n个未知数,使之在一定程度上更能适应有关极值问题的求解.
1 任意个因子的积的线性极大问题的推广
1 几个引理
引理1[1] 设X1 、X2 、X3 ……Xn是n个正变数,如果它们的和是定值,那么它们的积,当n个因子都相等时是极大.
引理2[1] 设X1 、X2 、X3 ……Xn满足线性方程
A1 X1+A2 X2 +A3 X3+……+AnXn=B,
其中系数A1 、A2、 A3 …… An以及B都是给定的正常数,那么积
P=X1 X2 X3……Xn ,
当A1 X1=A2 X2 =A3 X3=……=AnXn时是极大.
引理3[1] 如果正变量X1 、X2 、X3的和是定值,那么积X1x X2 x X2 x X3x X3x 当变量X1 、X2 、X3同指数x 当变量X1 、X2 、X3同指数x 、x 、x 、x 、x 成比例时是极大,其中x 成比例时是极大,其中x 、x 、x 、x 、x 是给定的正有理数. 是给定的正有理数.
引理4[1] 设正变量X1 、X2 、X3满足线性方程
A1 X1+A2 X2 +A3 X3=B,
其中A1 、A2、 A3及B都是给定的正常数,那么积
P =X1x X2 x X2 x X3x X3x , ,
当 = = = = 时是极大,其中x 时是极大,其中x 、x 、x 、x 、x 是正有理数. 是正有理数.
1.2 主要推广结果
定理1 若正变量X1 、X2 、X3 ……Xn的和是定值,那么积X1x X2 x X2 x X3x X3x ……Xnx ……Xnx 当变量X1 、X2 、X3 ……Xn同指数x 当变量X1 、X2 、X3 ……Xn同指数x 、x 、x 、x 、x ……xn成比例时是极大,其中x ……xn成比例时是极大,其中x 、x 、x 、x 、x ……xn是给定的有理数. ……xn是给定的有理数.
证明 因为x 、x 、x 、x 、x ……xn可能为正整数也可能为正分数,但无论哪种都可表示为正分数的形式,在这里我们把x ……xn可能为正整数也可能为正分数,但无论哪种都可表示为正分数的形式,在这里我们把x 、x 、x 、x 、x ……xn变成有最小公分母的D: ……xn变成有最小公分母的D:
x = = , x , x = = , x , x = = , …… , xn= , …… , xn= , ,
于是把积写成:
P=X1x X2 x X2 x X3x X3x ……Xnx ……Xnx =X1 =X1 X2 X2 X3 X3 ……Xn ……Xn = = , ,
可见得积P同积X1x X2 x X2 x X3x X3x ……Xnx ……Xnx 同时极大, 同时极大,
而积X1x X2 x X2 x X3x X3x ……Xnx ……Xnx 又同积 又同积
P = = =( =( ) ) ( ( ) )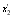 ( ( ) ) ……( ……( ) ) , ,
同时极大,但P 是x 是x + x + x + x + x +……x +……x 个正因子的积,而这些因子的和 个正因子的积,而这些因子的和
x  + x + x  + x + x  +……x +……x  =X1 +X2 +X3 +……+Xn=B, =X1 +X2 +X3 +……+Xn=B,
是定值,因此,由引理1知,积P 当 当 = = = = =……= =……= 时, 时,
即当 = = = = =……= =……= 时是极大,从而积P也当这时是极大. 时是极大,从而积P也当这时是极大.
定理证毕.
定理2 设正变量x 、x 、x 、x 、x ……xn满足线性方程 ……xn满足线性方程
A1X1+A2X2 +A3X3+……+AnXn=B, (1)
其中A1 、A2、 A3 …… An以及B都是给定的正常数,那么积
P = X1x X2 x X2 x X3x X3x ……Xnx ……Xnx , (2) , (2)
当 = = = = =……= =……= 时极大,其中x 时极大,其中x 、x 、x 、x 、x ……xn是正有理数. ……xn是正有理数.
证明 事实上我们有(2)可得:
P=  , ,
可见积P,同积
P = = , ,
同时极大.
因此,可令x = =  , x , x = =  , x , x = =  ,…… ,x ,…… ,x = =  , ,
那么(1)可化为:
X +X +X + X + X +……X +……X =B, =B,
是定值,因而由定理1知当 = = = = =……= =……= 时 时
即当 = = = = =……= =……= 时,积 时,积
X  X X  X X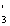  …… ……
1/3 1 2 3 下一页 尾页 |


