论文摘要:利用Banach压缩映射原理讨论非线性分数阶微分方程边值问题
论文关键词:压缩映射原理,格林函数,边值问题,微分
0引言:
分数阶微分方程在不同的科学领域起着越来越重要的作用。例如在扩散和运输理论、高分子材料的解链、弹性梁等诸多领域得以应用。近年来,有许多学者在分数阶微分方程领域取得了不少的成果.
本文受到文献[5]的启发,利用Banach压缩映射原理讨论下面含参数分数阶微分方程边值问题
解的存在性及唯一性,其中 是一个实数,并且 是一个实数,并且 是Caputo型微分。并假设 是Caputo型微分。并假设 是连续的。 是连续的。
1预备知识
为了方便证明,直接给出分数阶微分方程的定义和基本定理。
定义1.1:函数y: 的 的 阶Caputo型微分定义如下: 阶Caputo型微分定义如下:
 0 0
定义1.2:函数y: 的 的 阶Riemann—liouville型分数阶积分定义如下: 阶Riemann—liouville型分数阶积分定义如下:

引理1.1:令 ,那么分数阶微分方程 ,那么分数阶微分方程 有解 有解

其中
引理1.2:令 ,则有 ,则有
其中 0 0
由引理1.1,引理1.2可得下面的引理。
引理1.3:给定 ,且 ,且 ,则分数阶微分方程 ,则分数阶微分方程

的唯一解是 ,其中 ,其中
 (2) (2)
引理1.4:通过(2)定义的格林函数 有如下性质: 有如下性质:
(R1) ,而且对 ,而且对 ,有 ,有 ; ;
(R2) 0 0
令 ,其范数 ,其范数 ,可知(X, ,可知(X, )是Banach空间。 )是Banach空间。
在本文中做以下假设:
(H1)存在常数 ,使得 ,使得
考虑
定义算子T: 为: 为: ,则分数阶微分方程问题(1)有解,等价于算子方程 ,则分数阶微分方程问题(1)有解,等价于算子方程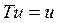 有不动点。 有不动点。
定理1.1(Banach压缩映射原理)设D是Banach空间X中的一个非空闭子集,而T: 0,且T在D内满足Lipschitz条件,即对任意的 0,且T在D内满足Lipschitz条件,即对任意的 ,有 ,有 ,则必存在唯一的 ,则必存在唯一的 ,使 ,使 。 。
2主要结果
定理2.1如果假设H1成立,且 , ,
那么边值问题(1)存在唯一解。
证明:令 , ,
定义空间 , ,
由(H1),对 ,有 ,有 . .
则
 
所以T: ,对 ,对 ,有 ,有
 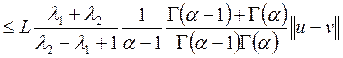
因为 ,所以T是压缩映射,于是存在唯一的 ,所以T是压缩映射,于是存在唯一的 ,即边值问题(1)存在唯一正解 ,即边值问题(1)存在唯一正解 。 。
参考文献
1 同登科,王瑞和,杨河山.管内非Newton流体分数阶流动的精确解[J].中国科学G辑,2005(3):318—326.
2 S.D.Eidelman and A.N.Kochubei.Cauchy problem for fractional diffusion equations[J].J.Diff.Eqns,2004(199):211—255.
3 V.D.Gejji,A.Babakhani. Analysis of a system of fractional differential equations [J].J.Math.Anal.Appl,2004(193):511—522.
4 AlvesEMaTF,PelicerMLMonotone positive solutions for a fourth order equation wh is nonlinear boundary conditions Nonlinear Analysis,2009;71:3834—3841.
5 Shuqin Zhang,Positive solutions for boundary_value Problems of nonlinear fractional differentialequations,Electronic Journal of Differential Equations,2006
6 Yinghan Zhang,Zhanbing Bai,Tingting Feng.Existence results for coupled system of nonlinear fractional three-pointboundary value problems at resonance[J]. Comput-
7 Chuan zhi Bai,Jinxuan Fang.The existence of a positive solution for a singular coupled system of nonlinear fractionaldifferential equations[J].Applied Mathematics and Computation, 2004 (150): 611–621.
8 苏新卫.分数阶微分方程耦合系统边值问题解得存在性[J],工程数学学报, 2009 (26):133–137.
|


