| eyimg293|。
分析:此题是黎曼引理的一个具体应用,其中取 ,由黎曼引理可得结论,这里我们用积分中值定理来证明结论。 ,由黎曼引理可得结论,这里我们用积分中值定理来证明结论。
证明: = = = =
= , ,  . .
=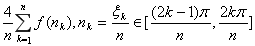
又 ,所以 ,所以 = = 。 。
4.在与收敛有关的问题中的应用
例7 设函数 , , 为正实数,证明: 为正实数,证明: 收敛并求其值。 收敛并求其值。
在 中有一个一般的结论,本文在 中有一个一般的结论,本文在 的基础上令 的基础上令 ,得到一个具体的结果。 ,得到一个具体的结果。
分析:我们先将 变为 变为 ,其次将 ,其次将 变形为 变形为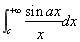  ,再利用变量代换将式子变形为 ,再利用变量代换将式子变形为 ,然后用积分中值定理即可证明。 ,然后用积分中值定理即可证明。
证明:令 = = = =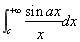  = =
= ,由积分中值定理,存在 ,由积分中值定理,存在 介于 介于 与 与 之间,使得 之间,使得 = = = = ,所以 ,所以 = = = = 收敛,且 收敛,且 =0 =0
参考文献
[1]华东师范大学数学系编.数学分析(上)第三版[M],217,222.北京:高等教育出版社,2002.
[2]王红军,李钓涛.积分第一中值定理的改进及其应用[J].商丘职业技术学院报,2004年第6期第3卷,22.
[3]程其襄等编.实变函数与泛函分析基础第二版[M],197. 北京:高等教育出版社,2003.
[4]裴礼文著.数学分析中的典型问题与方法[M],317,224,435,348,362,411,北京:高等教育出版社,2006.
[5]舒斯会著.数学分析选讲[M],115,北京:北京大学出版社.2007.
[6]刘三阳,李广民,于力等编.数学分析选讲[M],220,北京:科学出版社,2007.
[7]邓晓红.积分中值定理的应用[J],贵州金筑大学学报,总第55期第3期.118.
3/3 首页 上一页 1 2 3 |


