yimg150|虽然不一定连续,但导数具有介值性 ,因而由定理6得:存在唯一的点 ,因而由定理6得:存在唯一的点 ,使得 ,使得
 = = (4) (4)
将(4)式代入(3)即得
 ,即证。 ,即证。
2.在积分不等式证明中的应用
积分不等式是指不等式中含有两个以上积分的不等式,当积分区间相同时,先合并同一积分区间上的不同积分,根据被积函数所满足的条件,灵活运用积分中值定理,以达到证明不等式成立的目的。
例3若函数 在闭区间 在闭区间 上严格单调递减且连续, 上严格单调递减且连续, 的大小关系。 的大小关系。
在 中给出了函数 中给出了函数 在闭区间 在闭区间 上严格单调递增且连续的情况下的证明,本文则讨论 上严格单调递增且连续的情况下的证明,本文则讨论 在闭区间 在闭区间 严格单调递减且连续的情况。 严格单调递减且连续的情况。
分析:将 作差得 作差得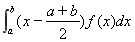 ,那么我们只要讨论 ,那么我们只要讨论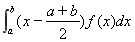 的值与“0”的大小关系即可。下面我们用三种方法来证明。 的值与“0”的大小关系即可。下面我们用三种方法来证明。
证明一:设函数 ,其中 ,其中 。显然在区间 。显然在区间 上,函数 上,函数 是单调递减且非负的,在区间 是单调递减且非负的,在区间 上,函数 上,函数 是单调递增且非负的。由定理2和定理3知, 是单调递增且非负的。由定理2和定理3知,  使得 使得  (5) (5) 使得 使得 (6) (6)
(6)-(5)得

= (7) (7)
又 使 使 ,且 ,且 ,由定积分的几何意义知 ,由定积分的几何意义知 ,因此,由(7)式得 ,因此,由(7)式得
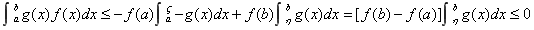
即  ,而 ,而 ,移项即有 ,移项即有 。 。
证明二:设函数 ,其中 ,其中 ,显然函数 ,显然函数 在区间 在区间 上可积,又函数 上可积,又函数 在区间 在区间 上递减连续,根据定理4可得,存在 上递减连续,根据定理4可得,存在
 (8) (8)
显然在区间 上,函数 上,函数 是单调递减且非负的,在区间 是单调递减且非负的,在区间 上,函数 上,函数 是单调递增且非负的,故(8)式可变为: 是单调递增且非负的,故(8)式可变为:

由定积分的几何意义知:
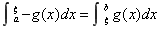 , ,
同时, ,于是 ,于是

即 。 。
证明三:取c=  ,再设 ,再设 , , 在 在 上单调递减连续,且 上单调递减连续,且 在 在 及 及 上不变号,由定理6得:存在唯一的 上不变号,由定理6得:存在唯一的 使得 使得
 ,这里 ,这里 ; ;
存在唯一的 使得 使得
 ,这里 ,这里 . .
且由于 在 在 上单调递减,所以 上单调递减,所以 。 。
而 ,故 ,故
 = =
即有 ,移项即有 ,移项即有 。 。
从上面的三种证明过程可以看出,证明一和证明二都是由积分中值定理得出的结论,而证明三是由定理6(即改进后的积分中值定理)得出的结论,比较两者我们不难看出定理6(即改进后的积分中值定理)的优越性。
例4 设 的导函数在[0,1]上连续,证明: 的导函数在[0,1]上连续,证明: 。 。
分析:将 拆分成 拆分成 ,又因为 ,又因为 的导函数在 的导函数在 上连续,所以 上连续,所以 在 在 必存在最大值点和最小值点,分别设为 必存在最大值点和最小值点,分别设为 ,那么我们可以得到 ,那么我们可以得到 = =  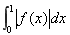 + + ,然后通过计算,由积分中值定理即证。 ,然后通过计算,由积分中值定理即证。
证明:记 = = , , ,则有 ,则有
   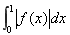 + + = = + +   + + (9) (9)
由积分中值定理,存在 ,使得 ,使得 = =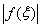 ,所以 ,所以 - -  ,故再由(9)式有 ,故再由(9)式有  .即证。 .即证。
3. 在与积分极限有关的问题中的应用
无论是在数列极限,还是函数极限的计算中,如果含有定积分式子,首先用定积分的相关知识,如积分中值定理等,把积分式简化,然后再运用解决极限问题的各种方法,就能达到解决问题的目的。
例5设 在[A,B]上连续, 在[A,B]上连续, ,求 ,求 . .
分析:此题在 中将 中将 变形为 变形为 ,然后用洛必达法则解得答案,本文我们可以将 ,然后用洛必达法则解得答案,本文我们可以将 变形为 变形为 ,再用变量代换变为 ,再用变量代换变为 ,然后用积分中值定理也可以得到相同答案。 ,然后用积分中值定理也可以得到相同答案。
解:
 = = = = = = = =   ,其中 ,其中 介于 介于 与 与 之间, 之间, 介于 介于 与 与 之间。所以当 之间。所以当 时,有 时,有 ,故 ,故 = = . .
例6 设 是[0,2 是[0,2 ]的连续函数,证明: ]的连续函数,证明: =|k =|k 2/3 首页 上一页 1 2 3 下一页 尾页 |


