论文导读::为什么要去分母一堂数学课教学后的反思,数学教学论文。
论文关键词:去分母,数学课
在新的数学课程标准中明确规定:“尊重学生的个体差异,倡导自主性学习和探究性学习,体现了数学学习活动的过程性特点”。北师大版义务教育课程标准实验教科书数学八年级下册第三章《分式》里面第4节〈分式方程〉,笔者在教学时发现教材上的解法和学生的解法有本质的区别,这节课上完后,我在课堂上定时出了几个练习题,发现全班有80%的同学都没有用教材上的解法,这是为什么呢?下课后我反复思考这个问题,是教材编写的问题,还是教师教学的问题,需要对教材作些什么样的改动呢?
二、课堂教学片断回放
数学课堂教学是数学活动的教学,是师生之间、学生之间交往互动与共同发展的过程。数学课堂教学,要紧密联系学生的生活实际,从学生的生活经验和已有知识出发,创设生动有趣的情境,引导学生开展观察、操作、猜想、推理、交流等活动,使学生通过数学活动,掌握基本的数学知识和技能,初步学会从数学的角度去观察事物、思考问题,激发学习数学的兴趣。
[师]在上节课的几个问题,我们根据题意将具体实际的情境,转化成了数学模型――分式方程.但要使问题得到真正的解决,则必须设法解出所列的分式方程.
这节课,我们就来学习分式方程的解法.我们不妨先来回忆一下我们曾学过的一元一次方程的解法,也许你会从中得到启示,寻找到解分式方程的方法.
解方程 + + =2- =2-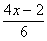
[师生共解](1)去分母,方程两边同乘以分母的最小公倍数6,得
3(3x-1)+2(5x+2)=6×2-(4x-2).
(2)去括号,得9x-3+10x+4=12-4x+2,
(3)移项,得9x+10x+4x=12+2+3-4,
(4)合并同类项,得23x=13,
(5)使x的系数化为1,两边同除以23数学教学论文数学教学论文数学教学论文,x= . .
讲解新课,探索分式方程的解法
[师]刚才我们一同回忆了一元一次方程的解法步骤.下面我们来看一个分式方程.(出示投影片
[例1]解方程: = =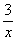 . (1) . (1)
[生]解这个方程,能不能也像解含有分母的一元一次方程一样去分母呢?
[师]同学们说他的想法可取吗?
[生]可取.
[师]同学们可以接着讨论,方程两边同乘以什么样的整式(或数),可以去掉分母呢?
[生]乘以分式方程中所有分母的公分母.
[生]解一元一次方程,去分母时,方程两边同乘以分母的最小公倍数,比较简单.解分式方程时,我认为方程两边同乘以分母的最简公分母,去分母也比较简单.
[师]我觉得这两位同学的想法都非常好.那么这个分式方程的最简公分母是什么呢?
[生]x(x-2).
[师生共析]方程两边同乘以x(x-2),得x(x-2) =x(x-2) =x(x-2)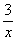 , ,
化简,得x=3(x-2). (2)
我们可以发现,采用去分母的方法把分式方程转化为整式方程,而且是我们曾学过的一元一次方程.
[生]再往下解,我们就可以像解一元一次方程一样,解出x.即x=3x-6(去括号)
2x=6(移项,合并同类项).
x=3(x的系数化为1).
[师]x=3是方程(2)的解吗?是方程(1)的解吗?为什么?同学们可以在小组内讨论.
(教师可参与到学生的讨论中,倾听学生的说法)
[生]x=3是由一元一次方程x=3(x-2)(2)解出来的,x=3一定是方程(2)的解.但是不是原分式方程(1)的解,需要检验.把x=3代入方程(1)的左边= =1,右边= =1,右边= =1,左边=右边,所以x=3是方程(1)的解. =1,左边=右边,所以x=3是方程(1)的解.
[师]同学们表现得都很棒!相信同学们也能用同样的方法解出例2. (出示投影片)
[例2]解方程 = = -2. -2.
(可让学生在练习本上完成,发现有和小亮同样解法的同学,可用实物投影仪显示他的解法,并一块分析)
[师]我们来看小亮同学的解法: = = -2 -2
解:方程两边同乘以x-3,得2-x=-1-2(x-3)
解这个方程,得x=3.
[生]小亮解完没检验x=3是不是原方程的解.
[师]检验的结果如何呢?
[生]把x=3代入原方程中,使方程的分母x-3和3-x都为零,即x=3时,方程中的分式无意义,因此x=3不是原方程的根.
[师]它是去分母后得到的整式方程的根吗?
[生]x=3是去分母后的整式方程的根.
[师]为什么x=3是整式方程的根,它使得最简公分母为零,而不是原分式方程的根呢?同学们可在小组内讨论.
(教师可参与到学生的讨论中,倾听同学们的想法)
[生]在解分式方程时,我们在分式方程两边都乘以最简公分母才得到整式方程.如果整式方程的根使得最简公分母的值为零,那么它就相当于分式方程两边都乘以零,不符合等式变形时的两个基本性质,得到的整式方程的解必将使分式方程中有的分式分母为零,也就不适合原方程了.
[师]很好!分析得很透彻,我们把这样的不适合原方程的整式方程的根,叫原方程的增根.
在把分式方程转化为整式方程的过程中会产生增根.那么,是不是就不要这样解?或采用什么方法补救?
[生]还是要把分式方程转化成整式方程来解.解出整式方程的解后可用检验的方法看是不是原方程的解.
[师]怎样检验较简单呢?还需要将整式方程的根分别代入原方程的左、右两边吗?
[生]不用,产生增根的原因是这个根使去分母时的最简公分母为零造成的.因此最简单的检验方法是:把整式方程的根代入最简公分母.若使最简公分母为零,则是原方程的增根;若使最简公分母不为零,则是原方程的根.是增根,必舍去.
[师]在解一元一次方程时每一步的变形都符合等式的性质,解出的根都应是原方程的根.但在解分式方程时,解出的整式方程的根一定要代入最简公分母检验.小亮就犯了没有检验的错误.
[师]总结解分式方程的一般步骤(出示投影片)
解分式方程一般步骤
1.去分母
2.解整式方程
3.检验
这节课看似乎很完美,既让学生主动参与了,又发展了学生的数感、符号感、以及应用意识与推理能力,本应完成了教学大纲的要求,但是学生作业却与之相反,这是为什么呢?
三、课后反思
教学反思,是教师对自己参与的教学活动的回顾、检验与认识,本质上是对教学的一种反省认知活动。教师以自己的实践过程为思考对象,在“回放过程”的基础上,对其中的成败得失及其原因进行思考,得到一定的能用以指导自己教学的理性认识,并形成更为合理的实践方案。因此,在目前基础教育课程改革的背景下对数学课堂教学进行反思就显得尤为重要。
上面的教学中,解分式方程第一步都是去分母,变为整式方程求解的。然后我们来看看学生的解法:
我布置了这样几个练习题,80%的同学都是下面这样解的:
(1)解方程 = =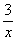
解:通分为 = =
所以
解得:
经检验 是原分式方程的解。 是原分式方程的解。
(2)解方程 - - =4 =4
解:通分为 - - = =
所以600-480=8
解得:
经检验 是原分式方程的解 是原分式方程的解
1/2 1 2 下一页 尾页 |


