【摘 要】幂级数是级数这一章的主要内容,求幂级数的和函数是一个非常重要运算,也具有一定的技巧性。文章结合多年的教学实践,介绍了求幂级数的和函数的最基本的方法。
【关 键 词】幂级数 和函数 积分 逐项求导 收敛域
求幂级数的和函数的思路是:经过加、减、乘运算,或逐项求导运算或逐项求积分运算,将幂级数转化为我们已知其和的幂级数(例如等比级数 从而求得原幂级数之和函数。以下通过举例说明求幂级数的和函数的基本方法。 从而求得原幂级数之和函数。以下通过举例说明求幂级数的和函数的基本方法。
例 求下列幂级数的和函数:
① ② ②
③ ④ ④
解:①先要求出和函数的定义域,即幂级数的收敛域。易得该幂级数的收敛域为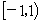 。再设 。再设 则逐项求导得 则逐项求导得
 
=
这是一个公比为 的几何级数,其和为 的几何级数,其和为

两边积分得
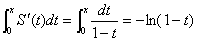  
而 = =
令 代入原幂级数 代入原幂级数 得S(x)=0。所以 得S(x)=0。所以

注意:代写硕士论文逐项求导后收敛区间的端点的收敛性可能会起变化,需要对端点进行讨论。
②幂级数的收敛域容易得出为(-1,1).
设 则逐项积分得 则逐项积分得

两边再求导得

注意:逐项积分后,收敛区间端点的收敛性可能会起变化。此刻当
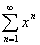 时均为发散,因此收敛域与收敛区间相同。 时均为发散,因此收敛域与收敛区间相同。
小节:从①②题可以得出一个思路,采用一种运算后使幂级数中 的系数变成1或 的系数变成1或
-1.这样就可以利用几何级数的求和公式,从而得出原幂级数之和。
③先求

得R= ,级数均为发散,所以幂级数的收敛域为(-1,1).令 ,级数均为发散,所以幂级数的收敛域为(-1,1).令

后一个幂级数为几何级数,得

前一个幂级数,要使其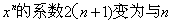 无关的常数,可用逐项积分的方法。令 无关的常数,可用逐项积分的方法。令

则

两边求导

即

④ 这是缺项幂级数。 这是缺项幂级数。

 幂级数发散,所以幂级数的收敛域为(-1,1)。 幂级数发散,所以幂级数的收敛域为(-1,1)。
设 
令
则
两边求导得
而

即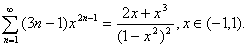
【 参考文献】
[1]盛祥耀,等.高等数学辅导.北京:高等教育出版社,2003.
[2]梁保松,等.高等数学.北京:中国农业出版社,2001.
[3]王信峰,大学数学简明教程.北京:高等教育出版社,2002.
[4]刘永莉,李曼生,两类幂级数的和函数的求法.甘肃联合大学学报(自然科学版),2005.(2).
[5]张绍璞, 一类幂级数的和函数与h(n,K)数的引入. 天津轻工业学院学报,1993(2).
[6]龚成红,幂级数的和函数.2003. |


