论文导读::在原有的积分中值定理的基础上加强了被积函数的条件得出了至少存在一点 属于开区间 属于开区间 的结论、给出了证明,并且应用到形如 的结论、给出了证明,并且应用到形如 这一问题的证明中,较为有效. 这一问题的证明中,较为有效.
论文关键词:积分中值定理,严格单调,开区间
0引言
积分中值定理是被积函数 在闭区间 在闭区间 连续的条件下得出至少存在一点 连续的条件下得出至少存在一点 属于闭区间 属于闭区间 使得式子 使得式子 成立的结论,有时利用该定理解决问题 成立的结论,有时利用该定理解决问题 能否在两端点取值至关重要,我们被积对函数作一限制开区间,得到 能否在两端点取值至关重要,我们被积对函数作一限制开区间,得到 的结论, 给出了证明,并且以证明 的结论, 给出了证明,并且以证明 这一问题为例来表明 这一问题为例来表明 的重要性. 的重要性.
1.相关的定义与定理
定义1.(严格单调) 设函数 设函数 在数集 在数集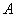 上有定义.若 上有定义.若  ,且 ,且 有 有
 ( ( ),则称函数 ),则称函数 在 在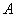 上严格增加(严格减少). 上严格增加(严格减少).
定理1.( 严格单调充分条件)  若函数 若函数 在区间 在区间 可导, 可导,  ,有 ,有 ( ( )则函数 )则函数 在区间 在区间 上严格增加(严格减少). 上严格增加(严格减少).
定理2. 若函数 在闭区间 在闭区间 连续, 连续, 可导开区间, 可导开区间,  ,有 ,有 ( ( )则函数 )则函数 在闭区间 在闭区间 严格增加(严格减少). 严格增加(严格减少).
证明: 不妨设 (同理可证 (同理可证 情形) 情形)
因为  , , 由定理1可得函数 由定理1可得函数 在开区间 在开区间 严格增加 严格增加  在 在 分别应用拉格朗日中值定理(定理见文献2)得到 分别应用拉格朗日中值定理(定理见文献2)得到
 (1) (1)
 (2) (2)
由(1)、(2)及 易得 易得

综上可得函数 在闭区间 在闭区间 严格增加,定理2得证.事实上我们证明了一个更一般的结论,即有如下推论. 严格增加,定理2得证.事实上我们证明了一个更一般的结论,即有如下推论.
推论1. 若函数 在区间 在区间 可导, 可导,  ,有 ,有 ( ( )且 )且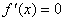
1/2 1 2 下一页 尾页 |


