论文导读:：本文给出了如何在直角坐标系下将三重积分交换次序的方法，即转化为二重积分在直角坐标系下交换次序的问题，并用实例进行了说明。
论文关键词：三重积分，二重积分，交换次序
一、问题的提出
二重积分在直角坐标系下交换次序，只需把积分区域分别看成 型和 型即可。但三重积分在直角坐标系下的次序有6种，它们分别是： 、 、 、 、 和 。由于积分区域是空间区域，往往很难想象，因此借助画出积分区域W的图形，完成三重积分在直角坐标系下交换次序通常不可行，需要新的方法解决这一问题。
二、交换三重积分在直角坐标系下次序的理论依据
确定三重积分的积分次序通常有两种办法，分别称为“投影法”和“截面法”。有的书上也称为“先单后重”和“先重后单”。
所谓“投影法”是指计算一个三重积分可以化为先计算一个定积分，再计算一个二重积分, 此二重积分的积分区域为W在坐标面上投影。
设空间闭区域 ，其中 为 在 平面上的投影。
则 【1】 ·(1)
若令
有 (2)
这样上的三重积分转化为上的二重积分。交换三重积分（1）中外层积分 的次序，只需交换积分区域为的二重积分(2)中的次序。
而“截面法”是指计算一个三重积分也可以化为先计算一个在截面上的二重积分，再计算一个定积分。设空间闭区域 ，其中 是竖坐标为 的平面截空间闭区域W所得到的一个平面闭区域中国论文下载中心。
则有  .【1】(3)
 (4)
则交换交换三重积分（3）中内层积分的次序，只需交换截面上二重积分（4）中的次序即可，此时应将变量看成常数。
若不是相邻交换，可用若干次相邻交换来实现。这样三重积分在直角坐标系下交换次序的问题二重积分，就转化为二重积分在直角坐标系下交换次序，从而问题得以解决。
三、举例说明
例将 按 的次序积分，再按 次序积分【2】。
解：1)按的次序积分，只需交换原积分中 的次序。由于是内层积分，，应将上面的积分看成是由截面法得到的，只需交换截面 上二重积分的次序即可。
把 看成常数，
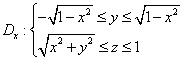
由此画出截面（见图1）
在平面区域上交换的次序 
 （5）
2）由前面分析知，交换次序时只能做相邻的交换，要换成次序积分，
可看成 两步组合而来。
而 已经完成, 即（5）。下面将（5）中外层积分 的次序交换。交换外层积分次序，应将此积分看成是由投影法得到的，只需交换投影区域 上二重积分的次序即可。
 ，由此画出积分区域（见图2）
在 平面交换次序得 
四、小结
由以上分析可知：三重积分在直角坐标系交换次序只能做相邻交换，对外层积分交换次序要把积分看成由投影法得到；对内层积分交换次序要把积分看成由截面法得到，从而转化为二重积分的交换次序；而对任意次序的交换，可用相邻交换实现。
参考文献：
[1]同济大学数学系编。高等数学第六版（下册）【M】6版，北京：高等教育出版社，2007：158-160
[2]詹锐清、卢海敏，高等数学全真课堂（上下册合订本）【M】，北京：学苑出版社，2002：580-581
|
