论文导读::求不定积分的过程比较复杂,没有一个统一的法则可以遵循。本文就不定积分运算中的一些灵活技巧给予了诠释。
论文关键词:不定积分,换元法,分部积分法,凑微分法
下面仅就不定积分运算中的一些灵活技巧给予诠释。
例1
求
解:原式= + + )dx )dx
=  =xtan =xtan +C +C
本题直接利用公式  = uv+c,从而免去了分部积分论文格式范文。 = uv+c,从而免去了分部积分论文格式范文。
例2求
解:原式= = = + + + + + +
=-cotxe +cscxe +cscxe +c +c
本题不仅利用了公式 =uv+c,同时在三角函数有理式处先使分母出现平方项凑微分法,再化简,这也是种有效的方法。 =uv+c,同时在三角函数有理式处先使分母出现平方项凑微分法,再化简,这也是种有效的方法。
例3求
解:原式=
=
又因为

= ,代入得: ,代入得:
= +c +c
在此例中利用了使分母出现平方项再化简的方法,从而使问题得以简化,当然有些问题直接利用第一凑微分法,二换元法也可。
例4求
解:原式= = =
利用了凑微分 = =
例5求
解:原式= (注:令 (注:令 ) )
=
= 
= 
= 
本例关键利用第二换元法 同时将 同时将 用 用 代换,从而使问题迎刃而解。可见代换也是求不定积分比较常用的一种方法。 代换,从而使问题迎刃而解。可见代换也是求不定积分比较常用的一种方法。
例6求
解:原式=
= = = + +
本例采用分子,分母同乘以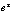 ,从而可凑微 ,从而可凑微 论文格式范文。一般情况下,当被积函数含有 论文格式范文。一般情况下,当被积函数含有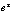 时凑微分法,上述凑微分法也是比较常见的。 时凑微分法,上述凑微分法也是比较常见的。
在不定积分运算中,不仅方法是多样的,而且灵活性也较强。那么在实际运算中究竟采用哪种方法,还要因题而宜。通过多做习题来不断积累经验,以求在掌握各种方法同时,灵活地运用它们。
[参考文献]
[1]李晓主编.高等数学[M]. 浙江大学出版社.
[2]李心灿主编.高等数学[M]. 高等教育出版社.
|


