AHP在学生学习成绩评价上的运用_定量.

论文导读:：本文针对现行的学生学习成绩评定过程中简单加权求和的不足，在引进定性函数将定量的分数定性化后，将现行的运筹学中的AHP方法运用在学生学习成绩上的评定过程中，有效区分学生成绩，从而使评定的结果更有说服力，更科学。
论文关键词：层次分析，AHP，学习成绩，评价，定性，定量.

 

0引言：

AHP（层次分析法）是系统工程中对非定量因素作定量分析的一种简洁的方法，它由F.L.Satay在70年代初提出以后，已经成功地运用经济，技术和政治等领域的系统分析和战略研究免费论文下载。AHP将哲学上的分解和综合的思维过程，采用数学的方法进行描述，建立决策过程的数学模型；因此具有实用性定量.，简洁性和系统性等优点，AHP的一般过程包括将问题概念化，建立递阶层次结构，构造一致性判断矩阵，层次因素排序和递阶综合排序等步骤。

1问题的提出

在现行的学校，在对学生的学习成绩进行评价的过程中，多是采用直接将各个学生的各门成绩相加，之后对所得的总成绩进行排序，这样做得的结果并不理想，也没有说服力，尽管有的学校在运用中对直接相加进行了改进，采取加权之后加和的方法来作为评定学生学习成绩的标准，但这种方法也有它自己的不合理性定量.，比如出现下面的情况；

现在从某班选取六个同学，要对他们的综合素质进行评定，我们选取其主要的五门成绩作为其评定的标准，其采集的各门成绩如下表1：

从表1我们可以看出，如果按现在多数学校实行的按总分累加来评定其学习成绩的话，明显是行不通的，因为所有的成绩总分都是350。也就说明他们的成绩是一样的，是分辨不出来的，但我们通过对上面的数据进行分析，可以看出，明显他们的学习成绩是不可能相同的，根本就不符合学习成绩为优的标准，即便是有的学校在评定过程中也考虑到了这些不合理定量.，引进了加权累加的方法，但在实际操作中还是有其不足的地方，比如在上面的评价中，相对来说，各门的成绩的权重应该是一样的，是不能区分的免费论文下载。从上面的案例可以看出现行的评价方法存在着其不合理性，必须选择一种更合理的，更科学的更具有说服力的方法来对学生

表1:学生各科成绩

的学习成绩进行评价，为此，我们可以引进AHP这种决策方法。在对上面的成绩运用AHP进行分析的时候，考虑到文中所说的直接运用成绩进行评判并不能完全反映各个学生的成绩的差异，故在本文中引进文中的定性函数 .对分数进行定量化之后再做AHP评判，在本文中依然令定量.，，，运用该函数对各个学生的分数进行定性化后数据为（表2）：
 

表2：学生成绩标准化后的数据

下面对经过定性化的数据进行AHP分析。
 

2AHP的运用

针对上面的综合评价方法的不可行性，我们下面引进AHP来对上面的学生的成绩进行综合评价，得出他们的综合评价次序免费论文下载。

第一步：建立递阶层次结构：

本文将不考虑将学生分组的情况，直接将学习成绩排序作为总体目标，将各门成绩作为准则，对各学生学习质量(即方案)排序。

第二步：构造一致性判断矩阵：

根据判断矩阵的构造方法，即针对某一个准则，将各个方案进行两两比较，在此题中就是将各个同学定性化后的成绩进行相比，得到如下的比较矩阵：（给出以制图为准则下各个方案两两比较得到的判断矩阵表3）

表3：制图标度下的比较判断矩阵

同理可得相对外语，数学定量.，材料，体育的定性判断矩阵。

以上求出相对各个准则下的各个方案的比较矩阵，对所得的矩阵还不能确定是否是一致性的矩阵，为此必须对其进行判定，对一致性的判定是致关重要的，不是一致性的矩阵，将对最终的评判结果产生很大的误差，一般的检验法则是求出比较矩阵的最大特征值，运用进行计算求得C.I，之后查表得出对应的值,若C.R=C.I/R.I的比值满足C.R<0.1，则认为其是一致性的矩阵，否则必须对其进行改进，关于矩阵的一致性的改进的方法请参看相关文献和书籍定量.，在此不多列免费论文下载。

对以上的一致性矩阵分别求出其最大特征值和对应的特征向量，由层次分析法的性质知道，如果其最大特征值等于其阶数，则其一定是一致性矩阵，

下面以制图为准则，对六个学生的成绩构成的比较矩阵进行求特征值及特征向量

特征向量矩阵特征值矩阵

从上面计算出的结果可以看出各个特征值对应着相应得特征向量，如特征值矩阵中6.0002为其对应得特征向量矩阵的第一列列向量。由层次分析法的知识知道，最大特征值对应得特征向量即为各个方案相对各个准则的排序，即相对制图来说六个学生的成绩排列为（0.4837， 0.1828 ，0.2974 0.1124，0.7867 ， 0.1124）

依次类推我们可以得到各个准则下的比较矩阵的特征向量矩阵和特征值向量矩阵,通过运算结果定量.，我们可以得到每个矩阵的特征值近似等于6，等于其维数，故可以得到各学科成绩排序权值分别为（表4）：

表4：各门成绩排序权值

通过以上的运算,我们得到了在各个准则下各个方案的排序，下面对各个准则下的向量进行归一化.即运用公式(,其中n为各个排序向量的分量个数)对各个准则下的向量进行归一化,如针对准则制图来说,对其排序向量利用上面的公式进行归一化后为:

其如类推,可以得出各个准则下的归一化排序向量,对其合并成一个矩阵得到如下矩阵：

以上的矩阵即是相对排序矩阵。

第三步：评价

我们依然是将各科相对于总体目标的权重看成是一样重要的，即相对于总体评价目标来说，制图，外语，数学，材料，体育的相对权重向量为

C=；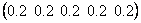

运用向量合成

C*B=*

=

以上的向量就是各个学生相对总的目标的排序，根据数值的大小等于各个方案相对总体目标的排序，可以得出六个学生的学习成绩排序分别为：第四个同学，第六个同定量.，第一个同学，第五个同学第二个同学，第三个同学。

这样就把六个同学的排序给计算出来了，这种方法相对于传统的累加方法是一种改进，也是合理的。

3．总结：

以上运用运筹学中的层次分析法对传统的成绩累加方法进行了改进，并将定量化的问题转化为定性的问题使得更能分辨出各个学生针对每门成绩的的差异，并对定性化后的比较矩阵进行AHP分析，使得综合测评效果更好，更具有说服力。

[参考文献]
[1]许树柏.层次分析[M],天津:天津大学出版社,1988
[2]徐泽水.判断矩阵一致性改进的一种实用方法[J],系统工程,16卷6期 1991.16(6)
[3]王中胜,李敏强,寇纪松.层次分析法判断矩阵不一致性的形成机理和一种修正方法[J],系统工程理论与实践 1995.9:36-43.
[4]刘宏宇,赵宏.AHP中定量准则的定性化问题 [J],系统工程,1989,13（6）
[5]Miroslaw Kwiesielewicz,Ewa van Uden. Inconsistentand contradictory judgements in pairwise comparisons method in the AHP[J]Computers&Operations Research. 2004,31: 713-719