| 6 钢管混凝土短柱承载计算分析
根据推导得出的承载力计算公式,针对几种特殊情况加以分析讨论,共分为六种特殊情况进行讨论。
6.1混凝土的泊松比趋近于零
当混凝土的泊松比趋近于零时,即 ,在轴压的作用下,混凝土的横向变形趋近于零,对钢管不产生径向的压力,故混凝土所受的围压为零,处于单向受压状态。则钢管所受到的内侧压力为零,也处于单向受压状态。钢管与混凝土之间没有作用力,故钢管对混凝土不产生约束效应。则钢管混凝土短柱所承受的荷载是钢管和混凝土分别所承受的荷载的线性叠加的结果。利用变形协调条件,钢管和混凝土在轴向的应变是相等的。由式(29)可得钢管混凝土短柱的极限承载能力的表达式为: ,在轴压的作用下,混凝土的横向变形趋近于零,对钢管不产生径向的压力,故混凝土所受的围压为零,处于单向受压状态。则钢管所受到的内侧压力为零,也处于单向受压状态。钢管与混凝土之间没有作用力,故钢管对混凝土不产生约束效应。则钢管混凝土短柱所承受的荷载是钢管和混凝土分别所承受的荷载的线性叠加的结果。利用变形协调条件,钢管和混凝土在轴向的应变是相等的。由式(29)可得钢管混凝土短柱的极限承载能力的表达式为:
 (30) (30)
由式(30)可以看出,当钢管与混凝土之间没有相互作用时,短柱的承载能力取决于钢管和混凝土的截面积及钢管的单轴抗压强度。
6.2混凝土的弹性模量趋近于零
混凝土的弹性模量趋近于零,即 时,由式(30)可得: 时,由式(30)可得:
 (31) (31)
由式(31)看出,此时,钢管混凝土短柱所承受的压力全部由钢管分担,混凝土几乎不起支承作用。
6.3钢管和混凝土的弹性模量和泊松比都相等
钢管和混凝土的弹性模量和泊松比都相等,即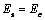 , , 时,则可将钢管混凝土短柱看作同单一材料的柱体结构,在单轴压缩条件下,极限承载力的表达式为: 时,则可将钢管混凝土短柱看作同单一材料的柱体结构,在单轴压缩条件下,极限承载力的表达式为:
 (32) (32)
由式(32)可以看出,在此条件下,短柱的极限承载力取决于横截面积和其单轴极限抗压强度的大小。
6.4钢管和混凝土的泊松比相等而其弹性模量不等
钢管和混凝土的泊松比相等,钢管弹性模量是混凝土弹性模量的k倍,即 , , ,在此条件下,钢管和混凝土符合变形协调条件,其轴向压缩应变相等建筑工程论文,又因为 ,在此条件下,钢管和混凝土符合变形协调条件,其轴向压缩应变相等建筑工程论文,又因为 ,故由此产生的横向应变也相同,则钢管壁和混凝土之间没有作用力,钢管对混凝土没有约束效应,即混凝土和钢管都处于单向受压状态。此时,其极限承载力的表达式为: ,故由此产生的横向应变也相同,则钢管壁和混凝土之间没有作用力,钢管对混凝土没有约束效应,即混凝土和钢管都处于单向受压状态。此时,其极限承载力的表达式为:
 (33) (33)
由式(33)可以看出,此时,钢管混凝土短柱的极限承载力主要取决于钢管的横截面积和单轴极限抗压强度,混凝土横截面积对短柱的极限承载力的影响较小。
由以上分析可知,在上述几种特殊情况下,承载力计算公式均可由 来表示。 来表示。
6.5钢管直径与壁厚的比值变化对承载力的影响
令 ,考虑 ,考虑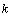 的变化对钢管混凝土短柱的极限承载力的影响,先分析系数 的变化对钢管混凝土短柱的极限承载力的影响,先分析系数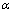 ,将 ,将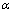 的分子分母同时除以 的分子分母同时除以 ,并化简,其分子化为: ,并化简,其分子化为:

其分母K可化为
 考虑k的大小对 考虑k的大小对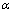 的影响,只需考虑分子分母的高次项,忽略低次项,则可得: 的影响,只需考虑分子分母的高次项,忽略低次项,则可得:
 (34) (34)
由式(34)可以看出,此时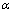 为定值,k的变化对 为定值,k的变化对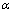 的影响较小,可以忽略掉。 的影响较小,可以忽略掉。
同理,可以推得k的变化对 的影响同样很小,可以忽略掉论文的格式。 的影响同样很小,可以忽略掉论文的格式。
因此,可以得出结论,k的变化对钢管混凝土短柱的极限承载力的影响较小,可以忽略。
6.6钢管混凝土短柱端面上混凝土凸出或凹进的影响
当钢管混凝土短柱的端面上混凝土凸出时,在轴压的作用下,混凝土最先承受压力,产生变形。此时,横向扩张变形受到钢管的约束,在钢管的作用下,混凝土处于三向受力状态,钢管只承受混凝土的反作用力,不承担轴向压力的作用。当混凝土的轴向变形足够大,其端面与钢管混凝土齐平时,才与钢管协同作用,共同承受轴向压力。
当钢管混凝土短柱的端面上混凝土凹进时,在轴压的作用下,钢管最先承受压力,产生变形建筑工程论文,导致横向变形,与混凝土脱离。此时,只有钢管承受轴压的作用,混凝土不起任何作用。当钢管端面与混凝土齐平时,钢管与混凝土才共同承担轴压的作用,由于钢管先产生变形,此时钢管的内壁与混凝土并没有接触,因此在这个阶段,钢管与混凝土都处于单轴受压状态。随着混凝土的横向变形和其内的微裂隙发展,导致混凝土与钢管弹性接触。混凝土受到钢管的约束作用,产生围压,进入三轴受压状态。此时,钢管与混凝土才协同作用,共同抵抗轴压。
6 结 论
(1)推导出了基于弹性变形理论的钢管混凝土短柱极限承载力计算公式: ,其中 ,其中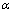 、 、 是与钢管和混凝土的弹性模量、泊松比、截面积有关的系数。 是与钢管和混凝土的弹性模量、泊松比、截面积有关的系数。
(2)当混凝土的泊松比趋近于零时,短柱的承载能力取决于钢管和混凝土的截面积及钢管的单轴抗压强度;
(3)混凝土的弹性模量趋近于零,钢管混凝土短柱所承受的压力全部由钢管分担,混凝土几乎不起支承作用。
(4)钢管和混凝土的弹性模量和泊松比都相等,短柱的极限承载力取决于横截面积和其单轴极限抗压强度的大小。
(5)钢管和混凝土的泊松比相等而其弹性模量不等时,钢管混凝土短柱的极限承载力主要取决于钢管的横截面积和单轴极限抗压强度,混凝土横截面积对短柱的极限承载力的影响较小。
(6)钢管直径与壁厚的比值变化对钢管混凝土短柱的极限承载力的影响较小,可以忽略。
参考文献(References):
[1]钟善桐.高层钢管混凝土结构[M] .哈尔滨:黑龙江科学技术出版社.1999(ZhongShantong. High residential encased structures[M]. Haerbin:Heilongjiang SciencePress,1999 (in Chinese).)
[2]蔡绍怀.现代钢管混凝土结构[M].北京:人民交通出版社,2003(Cai Shaohuai. Modern encased structures[M].Beijing: People’s Transportation Press,2003 (in Chinese).)
[3]韩林海.钢管混凝土结构-理论与实践[M].北京:科学出版社,2004(Han Linhai. Encased structures-theory and practices[M]. Beijing: Science Press,2004 (in Chinese).)
[4]韩林海,杨有福.现代钢管混凝土结构技术(第二版)[M].北京:中国建筑工业出版社,2007(Han Linhai, Yang Youfu. Modern encased structures technique[M].Beijing: China Constuction Industry Press,2007 (in Chinese).)
[5]袁文伯译.极限平衡法的结构承载力的计算[M].北京:建筑工业出版社,1958
[6]黄炎.工程弹性力学[M].北京:清华大学出版社,1982(Huang Yan. Engineering Elasticity) [M]. Beijing:Tsinghua University Press, 1982 (in Chinese).)
[7]刘鸿文.材料力学[M].北京:高等教育出版社,1992(Liu Hongwen. Mechanics of Materials[M]. Beijing:Hi Education Press, 1992 (in Chinese).)
3/3 首页 上一页 1 2 3 |


