论文导读::本文用指数多项式闭合或EPC(ExponentialPolynomial Closure)法分析了具非零均值响应的带位移偶次方项非线性随机振子在参数激励下响应的概率密度函数解。给出了求解过程并通过算例分析验证了指数多项式闭合法在此情况下的有效性。数值结果显示,指数多项式闭合法得到的响应概率密度结果与蒙特卡洛模拟的结果符合较好,尤其是在对系统可靠性分析起主要作用的概率密度函数尾部区域符合很好。
论文关键词:指数多项式闭合(EPC)法,Fokker-Planck方程,非零均值,位移偶次方非线性,参数激励
0 引言
科学和工程领域经常遇到非线性随机动力系统,所以关于非线性随机动力系统的概率求解问题在过去的几十年里一直受到人们的关注和研究。通常人们只研究带零均值响应的系统。但是在系统含有位移偶次方非线性项时,系统响应的均值非零。众所周知,当非线性振子受到白噪声激励时,系统响应的概率密度由Fokker-Planck方程控制。而求解Fokker-Planck方程是一个很具挑战性的问题。只有在非常严格的约束条件下才能得到一些稳态的精确解论文开题报告。目前最常用的方法是等效线性化(EQL)法[1][2]。EQL的限制条件是仅适用于弱非线性系统建筑工程论文,因为在弱非线性条件下系统的响应接近于高斯过程。为了提高解的精度,人们提出或采用了数种方法,如随机平均法[3][4]、Hermit多项式闭合法[5]、摄动法[6]、等效非线性法[7-9]、最大熵法[10][11]、有限差分法【12】,有限元法【13】,指数多项式闭合法(EPC)[14-16]等。随机平均法适于带弱阻尼和弱激励的系统;摄动法适于被摄动系统的解已知的情况;等效非线性法要求系统在一定统计意义下接近某一精确解已知的系统;最大熵法需要求解一复杂的非线性方程组;有限差分法和有限元法会带来概率密度函数尾部为负值的情况;Monte Carlo模拟法是适用性最广的方法[19][20],但对小概率的求解问题,它所需的计算量很大。指数多项式闭合法被提出之后,其有效性得到了一定程度的验证【14-18】。本文用指数多项式闭合法分析具非零均值响应的带位移偶次方项的非线性随机振子概率密度函数解,从而验证指数多项式闭合法在求解此类系统时的有效性。
1 指数多项式闭合法求解过程
考虑如下带参数激励的随机非线性振子:
 (1) (1)
式中 和 和 是系统响应的分量; 是系统响应的分量; 和 和 是 是 和 和 的非线性函数,其形式是确定的; 的非线性函数,其形式是确定的; 是零均值高斯白噪声,它的自相关函数为: 是零均值高斯白噪声,它的自相关函数为:
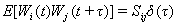 (2) (2)
这里 表示 表示 的期望值; 的期望值;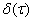 是Dirac函数; 是Dirac函数; 是相关谱密度。 是相关谱密度。
置 建筑工程论文, 建筑工程论文, ,式 (1) 可以表示为如下形式: ,式 (1) 可以表示为如下形式:
 (3) (3)
 (4) (4)
系统响应 和 和 是马尔科夫过程,式(4)中的第二项是Wong-ZaiKai修正项。其概率密度函数解由下面的Fokker-Planck 方程控制【21】: 是马尔科夫过程,式(4)中的第二项是Wong-ZaiKai修正项。其概率密度函数解由下面的Fokker-Planck 方程控制【21】:
 (5) (5)
其中 这里只考虑Fokker-Planck 方程的稳态解,此时方程(5)退化为: 这里只考虑Fokker-Planck 方程的稳态解,此时方程(5)退化为:
 (6) (6)
这里假设振子 (1) 的概率密度函数解在 中是连续的且满足下列要求: 中是连续的且满足下列要求:
 (7) (7)
将方程 (6) 的解表示为[15]:
 (8) (8)
其中 是归一化常数,a 是有 是归一化常数,a 是有 个参数的未知向量。而且 个参数的未知向量。而且
 (9) (9)
这是一个关于 和 和 的n阶多项式。为了满足条件 (7),令 的n阶多项式。为了满足条件 (7),令
 (10) (10)
其中  , , 和 和 (i=1,2)是系统响应的均值和标准差,是通过等效线性化法得到的; (i=1,2)是系统响应的均值和标准差,是通过等效线性化法得到的; 和 和 (i=1,2)是常数,通常设置为4。 (i=1,2)是常数,通常设置为4。
一般来说,由于式 (8) 只是方程 (6) 的近似解,而且a中的未知参数数量有限建筑工程论文,所以Fokker-Planck方程不能得到精确满足。把式(8) 代人方程 (6) 后产生的误差为:
 (11) (11)
由于 ,所以满足方程 (11)解的唯一可能性就是 ,所以满足方程 (11)解的唯一可能性就是 ,但是由于 ,但是由于 只是近似解,所以通常 只是近似解,所以通常 论文开题报告。在这种情况下,引入一组 论文开题报告。在这种情况下,引入一组 空间的基函数 空间的基函数 ,使得 ,使得 在 在 上的投影为零,即 上的投影为零,即
 (12) (12)
这意味着如果  在 在 空间上可积且方程组 (12) 可解,那么 空间上可积且方程组 (12) 可解,那么 在弱意义上满足了Fokker-Planck方程。 在弱意义上满足了Fokker-Planck方程。 的表达式可以取为 的表达式可以取为
1/2 1 2 下一页 尾页 |


