论文导读::为解决工程中得到广泛应用的钢管混凝土结构承载力计算问题,在总结分析已有钢管混凝土短柱承载力计算理论的基础上,利用弹性变形理论,推导出了钢管混凝土短柱极限承载力计算公式,利用推导得出的计算公式,对混凝土的泊松比趋近于零、混凝土的弹性模量趋近于零、钢管和混凝土的弹性模量和泊松比都相等、钢管和混凝土的泊松比相等而其弹性模量不等、钢管混凝土短柱端面上混凝土凸出或凹进的影响等六种条件下,钢管混凝土结构的承载情况进行了分析。
论文关键词:钢管混凝土短柱,弹性变形理论,承载力计算
0 引 言
钢管混凝土结构把钢和混凝土两种材料组合成一个整体,充分发挥了两种材料优势,不仅增强了钢管的局部稳定性,还提高了混凝土的强度,在工程中得到了比较广泛的应用。在进行钢管混凝土结构设计时,钢管混凝土构件的承载力计算是一个非常重要的环节,钢管混凝土构件既不同于混凝土构件,又不同于材质均匀的纯钢构件,它是一种具有组合受力特性的复合材料。因此它的承载能力的计算应当是建立在两种基本组成材料——钢和混凝土作用分担之上的一种新的计算方法。
数值分析法是一种精确的计算方法,能从理论上准确地描述钢管混凝土压弯构件的工作机理和性能,但单元选取难,计算较为复杂,用它来解决工程中的钢管混凝土计算问题不现实,关于钢管混凝土承载力的计算方法,主要有四种理论,即统一理论、拟混凝土理论、拟钢理论以及叠加理论。
统一理论主要基于哈尔滨工业大学和福州大学等研究成果[1][3-4],把钢管混凝土视为统一的一种组合材料,不再区分钢管和混凝土,通过试验回归得到组合材料的性能指标。拟混凝土理论即中国建筑科学院提出的约束混凝土理论[2],拟混凝土理论认为钢管混凝土本质上就是由钢管对混凝土实行套箍强化的一种套箍混凝土建筑工程论文,由于钢管对核心混凝土的套箍作用,使核心混凝土处于三向受压状态,从而使核心混凝土具有更高的抗压强度和变形能力,而对于钢管壁,将其视为分布在核心混凝土周围的等效纵向钢筋,钢筋的面积根据钢管的截面积和形状而定,因此,采用极限平衡理论[5]的方法推导出钢管混凝土轴压短柱的极限承载力公式。拟钢理论是同济大学基于钢结构分析方法提出了等效钢柱计算理论。拟钢理论是将混凝土折算成钢,把钢管混凝土看成受力钢构件,再按照钢结构规范的模式进行分析计算。
本文在总结分析已有的钢管混凝土短柱承载力计算理论的基础上,推导得出了基于弹性变形理论的钢管混凝土短柱极限承载力计算方法。
1 计算模型
建立钢管混凝土短柱的力学模型,利用弹性力学的计算方法,对其极限承载力进行分析计算。钢管混凝土短柱力学模型的基本假设为:
(1)钢管和混凝土都是线弹性材料;
(2)在变形过程中钢管和混凝土横向保持弹性接触;
(3)钢管混凝土短柱的强度取决于钢管的强度,钢管强度符合莫尔强度理论;
(4)在钢管的厚度方向上,钢管内的径向应力成线性分布,周向应力为均匀分布。

图1 钢管混凝土短柱力学模型
Fig 1 Calculative model of carrying capacity for Concrete-Filled Steel Tube puncheon

图2混凝土单元受力状态
Fig 2 Stress state in one point for concrete

图3 钢管混凝土短柱横断面
Fig 3 cross section of Concrete-Filled Steel Tube puncheon
如图1所示的钢管混凝土短柱,设其外径为 ,钢管的壁厚为 ,钢管的壁厚为 ,钢管和混凝土的横截面积分别为 ,钢管和混凝土的横截面积分别为 、 、 ,钢管的弹性模量和泊松比分别为 ,钢管的弹性模量和泊松比分别为 ,其单轴极限抗拉强度为 ,其单轴极限抗拉强度为 ,单轴抗压强度为 ,单轴抗压强度为 。混凝土的弹性模量和泊松比分别为 。混凝土的弹性模量和泊松比分别为 。对混凝土施加轴压 。对混凝土施加轴压 ,设钢管承受的压力为 ,设钢管承受的压力为 ,混凝土承受的压力为 ,混凝土承受的压力为 论文的格式。则 论文的格式。则 ,故 ,故 。钢管和混凝土都是线弹性的,在受到轴向压力时,钢管和混凝土在横向上保持弹性接触,可得 。钢管和混凝土都是线弹性的,在受到轴向压力时,钢管和混凝土在横向上保持弹性接触,可得
 (1) (1)
 (2) (2)
式中, 分别表示钢管和混凝土的轴向应变, 分别表示钢管和混凝土的轴向应变, 分别表示钢管和混凝土的径向位移。 分别表示钢管和混凝土的径向位移。
2 混凝土与钢管的轴向应变
由于钢管和混凝土的轴向压缩应变相等,即 。分别导出钢管和混凝土的轴向应变的表达式。 。分别导出钢管和混凝土的轴向应变的表达式。
2.1 混凝土的轴向应变
分析混凝土,在混凝土内取单元体,则其受力状态如图2所示,受轴压 和围压 和围压 的作用,则由胡克定律[6]可得: 的作用,则由胡克定律[6]可得:
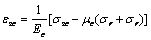
即, (3) (3)
2.2 钢管的轴向应变
钢管圆周方向的拉应力与变形是由于其内部混凝土横向变形引起的。在钢管内取单元体,则其受力状态如图4所示, 表示轴向应力, 表示轴向应力, 表示环向应力, 表示环向应力,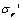 表示径向应力,由胡克定律可得: 表示径向应力,由胡克定律可得:
 (4) (4)

图4钢管单元受力状态图
Fig 4 Stress state in one point for steel tube

图5单元长度钢管混凝土短柱
Fig 5 Unit length of Concrete-Filled Steel Tube
取单位长度钢管混凝土短柱,如图5所示建筑工程论文,由静力平衡条件得

推得:
 (5) (5)
在钢管壁上,沿着径向,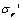 不是均匀分布的,由于钢管壁很薄,可以将其看作呈三角形分布,通过积分,可得 不是均匀分布的,由于钢管壁很薄,可以将其看作呈三角形分布,通过积分,可得 ,则有: ,则有:
 (6) (6)
2.3钢管与混凝土轴向应变相等条件
由 ,得: ,得:
 (7) (7)
将 , , 代入式(7)得出如下方程: 代入式(7)得出如下方程:
1/3 1 2 3 下一页 尾页 |


