 基于数形结合的解题案例分析 基于数形结合的解题案例分析
论文关键词:数形结合,解题案例,分析
问题:已知 求证: 求证: . .
证明: 解法1(分析法)
若证
只需两侧平方得:

由于  + + = = + +
即要证 
即  显然成立,故得证. 显然成立,故得证.
评析: 解法1中最关键的是第二步——对不等式两侧分别平方。对不等式进行平方的目的是为了出现和利用关系式(3)。即在整个证明过程中,起关键作用的实质步骤是第三步。那么,由(3)式你能看到什么?你能想到什么几何图形?你是否想到了有一公共斜边的两直角三角形?这一想法可能就会促使我们得到一个几何解法。

图1 图
解法1.1
分析:令 ,构造图形1。要证明 ,构造图形1。要证明 ,意味着需要找边之间的关系,图形1并未为我们提供太多边之间的关系,怎么办?改进它。将 ,意味着需要找边之间的关系,图形1并未为我们提供太多边之间的关系,怎么办?改进它。将 与 与 放在同一个半圆中,得到图 放在同一个半圆中,得到图 。 。
在图 中我们看到问题变成要证明:在同一个半圆中的两个直角三角形,直角边长相差越小,它们的和越大。这个结论正确,但不明显,需给出几何证明。 中我们看到问题变成要证明:在同一个半圆中的两个直角三角形,直角边长相差越小,它们的和越大。这个结论正确,但不明显,需给出几何证明。
证明:令 ,作图 ,作图 . .
由于  
而 

又  = =  
即.
解法2(直接证明)
由于 
  + + > >
  < <
即  < < (4) (4)
  
评析:解法2中最关键的是第一步——分子有理化。分子有理化的实质是 - - =1, =1, - - =1.那么,由这两个式子你看到了什么,它们又让你想到了什么图形?你能否联想到有一公共直角边的两个直角三角形?你能否看出在形式上它们又是双曲线上的两个点?波利亚说:"在解题中能有一个念头就很幸运了","我们应感谢所有的念头"。去实践这些念头,我们可能会得出新的解法。 =1.那么,由这两个式子你看到了什么,它们又让你想到了什么图形?你能否联想到有一公共直角边的两个直角三角形?你能否看出在形式上它们又是双曲线上的两个点?波利亚说:"在解题中能有一个念头就很幸运了","我们应感谢所有的念头"。去实践这些念头,我们可能会得出新的解法。    
图2 图3 图 图 图
解法2.1
分析:根据我们的第一个念头,构造有一公共直角边的两直角三角形。易得出图2,图3。
上面哪个图形更利于我们解题呢?回到题目上。证明 ,实质上是证三角形边之间的不等关系,两个图形分别呈现了两个相对独立的直角三角形(仅有一公共直角边)。想办法去改进它!将三角形放在同侧试一下,得出图形 ,实质上是证三角形边之间的不等关系,两个图形分别呈现了两个相对独立的直角三角形(仅有一公共直角边)。想办法去改进它!将三角形放在同侧试一下,得出图形 。这样做时,我们会发现图形 。这样做时,我们会发现图形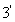 给我们提供了一个漂亮的几何证法。 给我们提供了一个漂亮的几何证法。
证明:构造图形 .令 .令 . .
在 中, 中, ,即 ,即 .故 .故 . .
  
图4 图5 图
解法2.2
分析: 根据我们的第二个念头,构造双曲线.得出 (图4)和 (图4)和 (图5)的图象。那么应选哪一个图形呢?这要看我们想利用图形给我们提供的什么信息。回到原题目。要证 (图5)的图象。那么应选哪一个图形呢?这要看我们想利用图形给我们提供的什么信息。回到原题目。要证 ,但我们看不出有关双曲线的任何迹象,是我们的数学功底不足还是题目本来就无法与双曲线联系?无法改变图形,我们可以试着对问题本身进行变形,得到 ,但我们看不出有关双曲线的任何迹象,是我们的数学功底不足还是题目本来就无法与双曲线联系?无法改变图形,我们可以试着对问题本身进行变形,得到 .再进一步得到 .再进一步得到 .现在你能想到什么?双曲线上两点所确定的直线的斜率。那么“1”代表什么呢?双曲线渐近线的斜率。这样就联系起来了。图形给我们提供这样的信息了吗?双曲线夹在两渐近线之间。并且此时我们会很自觉的选择图形5,因为在图4中存在着双曲线上两点直线斜率不存在的情况。 .现在你能想到什么?双曲线上两点所确定的直线的斜率。那么“1”代表什么呢?双曲线渐近线的斜率。这样就联系起来了。图形给我们提供这样的信息了吗?双曲线夹在两渐近线之间。并且此时我们会很自觉的选择图形5,因为在图4中存在着双曲线上两点直线斜率不存在的情况。
证明:如图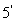 ,作双曲线 ,作双曲线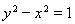 .在双曲线一支上任取两点 .在双曲线一支上任取两点 , , .连接 .连接 ,则 ,则 .即 .即 = = . . >0,所以 >0,所以 ,即 ,即 . .
回顾我们的解题历程,是对代数解法本质步骤的把握让我们产生了几何解法的念头,是解题目标的指引让我们对几何图形或问题本身不断进行变形,找到了几何解法。
|


