解:设y = = ,y ,y =1, 在直角坐标系中分别作出这两个函数的图象(如图1),原不等式的解集应为满足函数y =1, 在直角坐标系中分别作出这两个函数的图象(如图1),原不等式的解集应为满足函数y = = 的图 象 。在函数y 的图 象 。在函数y =1 的图象的下方的x的取值集合,求出方程 =1 的图象的下方的x的取值集合,求出方程 =1的解,易知原不等式的解集为{x =1的解,易知原不等式的解集为{x < x < < x <   }。 }。
我们运用数形结合的思想来解决问题,看似并没有显出比普通方法有多大的优越性,但是如果我们把题目稍微改一下的话,就会发现,利用数形结合是非常方便的。
图1
2.3求最值问题
求函数最值的方法较多,如直接法,单调性法,换元法,数形结合法等等。其中应用数形结合的思想方法,通过对函数解析式的剖析,构造适当的几何图形,创设相关的几何问题环境,利用某些几何量(如距离,直线斜率,截距等)的变化范围求函数的最值,常能起到化难为易,化繁为简的效果。
例 1 求函数y= + + + + 的最小值 的最小值
分析:利用数轴,根据 的几何意义是表示有向线段的长度进行研究。 的几何意义是表示有向线段的长度进行研究。
解析:在数轴上研究x所对应的动点P与1方法,2,3 所对应的
 点A, B, C相应的位置(如图2—1) 点A, B, C相应的位置(如图2—1)
   , , 
 
 当 P点与B点重合时,y 最小,且 当 P点与B点重合时,y 最小,且
 = = =2 。 =2 。  y 的最小值为2 。 y 的最小值为2 。
评析:根据数轴上有向线段的长度公式来研究这类绝对值问题十分直观、简捷。
例 2 求f(x)= 的最大值与最小值。 的最大值与最小值。
分析:函数解析式类似斜率公式,可引入新变量,构造相关的几何图形。
解:令x=cos , y=sin , y=sin , 则x , 则x + +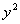 =1,且 f(x)= =1,且 f(x)=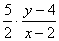 ,设k= ,设k=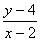 ,则表示过圆x ,则表示过圆x + +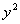 =1上一点P(x,y)与点M((2,4)的直线斜率(如图2—2),设过点M,P的直线L方程为y-4=k(x-2), 即kx-y+4-2k=0.当直线与圆相切时,有 =1上一点P(x,y)与点M((2,4)的直线斜率(如图2—2),设过点M,P的直线L方程为y-4=k(x-2), 即kx-y+4-2k=0.当直线与圆相切时,有 =1 . =1 .
  , ,  . .
 
 图3—2 图3—2
2.4 利用数形结合思想求方程的解的个数
例 1 求方程2 = = 的实数解的个数 的实数解的个数
解析:如图3—2,在同一坐标系内分别作出y=2 与y= 与y= 的图象,,两图象交点的个数即为所求论文开题报告。其中y=2 的图象,,两图象交点的个数即为所求论文开题报告。其中y=2 的图象随着x增大,图象趋于与y轴平行,故它有3个交点,所以解的个数为3个。含有两个或两个以上不同的函数(指数函数,对数函数,三角函数,反三角函数等0的综合方程,一般无法直接转化为代数方程来解,借助数形结合思想,给出其对应的函数图象,视方程的实根为函数图象的交点,则实根个数一目了然。 的图象随着x增大,图象趋于与y轴平行,故它有3个交点,所以解的个数为3个。含有两个或两个以上不同的函数(指数函数,对数函数,三角函数,反三角函数等0的综合方程,一般无法直接转化为代数方程来解,借助数形结合思想,给出其对应的函数图象,视方程的实根为函数图象的交点,则实根个数一目了然。
3.数形结合思想的教学方法
数形结合是数学中最重要也是最基本的思想方法之一。每种数学思想方法的形成都不是朝夕之间的,因此我将数学学科特点与学生认知特点相结合,有目的、有计划地设定数形结合思想的分层教学目标。
3.1渗透
以具体知识为载体,数形结合思想融入其中,使学生对数形结合有一些初步的感知
和直觉,帮助学生对知识的理解与记忆,培养学生有意识记与理解识记。
3.2揭示
以“轨迹”、“函数及其图形”,“解直角三角形”、“图”等内容为载体,向学生“点破阐释”、“突出地位”、“提炼概括”。使学生初步理解:“坐标法”即建立坐标系,把几何问题转化为代数问题,或把代数问题转化为几何问题,即几何问题代数化方法,图形性质坐标化。
“代数证法”即采用代数方法通过计算证明几何命题,“三角函数法”即把几何中有些线段与角的求解间题转化为三角函数问题也是儿何中常用的方法。把形转化为数,用数量关系研究图形位置关系,使学生获得解决问题的经验,形成技能,领悟数形结合的思想。
3.3强化
美国心理学家斯金纳提出:行为之所以发生变化,是由于强化作用,学生要获得有效的数学学习就必须通过“强化”。桑代克说:一个已形成的可变连结,若加以应用,就会变强;一个已形成的可变连结,若久不应用,就会变弱。教学要注意连续性,要经常地予以强调,并通过大量的综合而达到灵活运用。通过过强化训练,有利于学生掌握如何解决新问题的方法,再经积累、概括、总结,不断获得创造性数学活动的经验,从而形成一定的数学能力。
参考文献
[1]王俊平;数形结合的原则与途径[J]. 高中数学教与学 2006年02期 [2] 郑传枝; 用图象解题的两个注意点[J]. 高中数学教与学 2006年06期 [3] 黄坚; 加强数形结合 提高解题能力[J]. 广西教育 2004年29期 [4] 王颖; 浅析“数形结合”的数学教育意义[J]. 教学与管理 2004年36期 [5] 陈顺娘; 数学思想方法的教学实施[D]. 福建师范大学 2005 [6] 庞明石; 指导高中生数学解题策略的理论与实践[D]. 山东师范大学 2006 [7] 蒋诗泉; 高中数学有效教学策略研究[D]. 天津师范大学 2008 [8] 余霞辉; 高中数学解题中的化归方法及其教学研究[D]. 湖南师范大学 2007
2/2 首页 上一页 1 2 |


