论文导读::数形结合在教学中的作用。教师在数学教学活动中。借助于数形结合的方法给出增减函数的定义。应用“数形结合”体现数学之美育。
论文关键词:数形结合,教学,方法,应用
1.数形结合在教学中的作用
1.1应用“数形结合”体现数学之美育
例如:(1)在数与形的关系中特别引人注目的著名的“黄金分割率”,它被世人称之为和谐性的最完美的表现。“0.618”被誉为黄金数、神圣的比例、宇宙的美神。
(2)方程ρ=a(1-cosθ)的图形是心形线,如图1,
方程ρ=2asin3θ的图形是三叶玫瑰线,如图2。
 
图1图2
教师在数学教学活动中,要充分运用这些材料,引导学生领略数学的美,使学生对数学产生强烈的情感、浓厚的兴趣和探讨的欲望。
1.2.数形结合有助于知识的理解记忆。
 例如:在研究函数时,可以利用函数图形来记忆有关函数的知识点,像函数的定义域、值域、单调性、奇偶性、周期性等。这样,材料的组成方式较好,内容的组织结构较严密,记时可以提纲挈领地在大脑中储存,今后可以随时纲举目张地提取,达到良好的记忆效果。 例如:在研究函数时,可以利用函数图形来记忆有关函数的知识点,像函数的定义域、值域、单调性、奇偶性、周期性等。这样,材料的组成方式较好,内容的组织结构较严密,记时可以提纲挈领地在大脑中储存,今后可以随时纲举目张地提取,达到良好的记忆效果。
图3
如图3是余弦函数y=sinx的图象方法,从中我们可以知道正弦函数的定义域是(-∞,+∞),值域是[-1,1],函数在(2kπ-π/2,2kπ+π/2))内单调递增,在(2kπ+π/2,2kπ+3π/2)内单调递减,函数的周期是2π,函数关于圆点对称是奇函数,
1.3应用数形结合训练直觉思维能力
例1.如果实数 满足等式 满足等式 ,那么 ,那么 的最大值是什么? 的最大值是什么?
 解:设点 解:设点 在圆 在圆 上,圆心为 上,圆心为 ,半径等于 ,半径等于 。如图,则 。如图,则 是点 是点 与原点连线的斜率。当 与原点连线的斜率。当 与⊙ 与⊙ 相切,且切点 相切,且切点 落在第一象限时, 落在第一象限时, 有最大值,即 有最大值,即 有最大值。因为 有最大值。因为 = = , , = = ,所以 ,所以  = = = = ,所以 ,所以 = =  = = 论文开题报告。 论文开题报告。
例 2: 已知关于x 的方程 =px,有 4个不同的实根, 求实数p 的取值范围。 =px,有 4个不同的实根, 求实数p 的取值范围。
分析: 设y = = = 与y=px这两个函数在同一坐标系内, 画出这两个函数的图像, 如图4。可知: 与y=px这两个函数在同一坐标系内, 画出这两个函数的图像, 如图4。可知:

图4
(1)直线y= px 与y= -(x - 4x+ 3) , x - 4x+ 3) , x [ 1, 3 ]相切时原方程有3个根。 [ 1, 3 ]相切时原方程有3个根。
(2) y= px 与 x 轴重合时, 原方程有两个解, 故满足条件的直线y=px 应介于这两者之间, 由: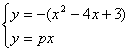 得 得
x + (p - 4)x+ 3= 0, 再由△=0 得, p = 4±2 + (p - 4)x+ 3= 0, 再由△=0 得, p = 4±2 , 当p= 4+ 2 , 当p= 4+ 2 时,x= - 时,x= -   [1, 3 ]舍去, 所以实数p的取值范围是 0<p< 4- 2 [1, 3 ]舍去, 所以实数p的取值范围是 0<p< 4- 2 。 。
处理方程问题时,把方程的根的问题看作两个函数图像的交点问题;处理不等式时,从题目的条件与结论出发,联系相关函数,着重分析其几何意义,从图形上找出解题的思路。
2.数形结合在教学中的应用
2.1数形结合在概念教学中的应用
在学习函数的单调性中,借助于数形结合的方法给出增减函数的定义。
首先引导学生观察下列函数的图像(三组)
问题1:指出各组图像有什么共同的特征?
第一组:
第二组:

第三组:
  
图8
观察得到:随着x的增大,函数的图像有的呈逐渐上升的趋势,有的呈逐渐下降的趋势,有的在一个区间内呈逐渐上升的趋势, 有的在另一个区间内呈逐渐下降的趋势,
问题2:你能明确地说出“图像呈逐渐上升的趋势”的意思吗?(从形到数)
讨论得到:
在某一区间内,
图像在该区间内呈逐渐上升的趋势 当x的值增大时,函数值y也增大; 当x的值增大时,函数值y也增大;
图像在该区间内呈逐渐下降的趋势 当x的值增大时,函数值y反而减小。 当x的值增大时,函数值y反而减小。
问题3:如何用数学语言来准确地表述函数的单调性呢?
引导学生讨论得到:
如果对于属于定义域I内某个区间上的任意两个自变量的值x1,x2,当x1<x2时,都有f(x1 )<f(x2 ),那么就说在这个区间上是增函数。
如果对于属于定义域I内某个区间上的任意两个自变量的值x1,x2方法,当x1<x2时,都有f(x1 )>f(x2 ),那么就说在这个区间上是减函数。
2.2数形结合在解题教学中的应用
例1:解关于x的不等式 <1 <1
分析:解含绝对值的不等式的关键是如何去掉绝对值符号,去绝对值符号的方法有很多种,如“不等式两边同时非负时,两边平方”,也可以利用分类讨论的思想来解决问题,还可以利用含绝对值不等式的性质。如:“ 〈 a 〈 a -a<f(x)<a , -a<f(x)<a , >a >a f(x)>a或 f(x)<-a(其中a>0)”,此题我们通常运用后面一种方法,转化为求两个不等式的交集。 f(x)>a或 f(x)<-a(其中a>0)”,此题我们通常运用后面一种方法,转化为求两个不等式的交集。
1/2 1 2 下一页 尾页 |


