| Akerlof等(1996)的更近研究中，对这种观点作了进一步地详细阐述。实证方面，Laxton等(1995,1999)、Alvarez-Lois(2000)、Gerlach(2000)等学者也给出了一些欧洲国家和美国存在凸性Phillips曲线的支持性证据。鉴此，下面通过在经济结构模型中引入凸性Phillips曲线，但仍保留对称的平方损失函数形式，在此新的分析框架下来检验有关最优利率规则的性质。
(一)非线性Phillips曲线
关于非线性Phillips曲线的形状并没有一致的观点，Laxton等(1995,1999)、Alvarez-Lois(2000)、Gerlach(2000)给出了凸的非线性，而Stiglitz(1997)、Eisner(1997)则给出了一个凹的曲线关系，但大部分研究表明Phillips曲线具有凸函数特征。这里，我们采取 的凸函数形式。凸Phillips曲线方程如下：
 (5)
其中，参数 >0，代表产出缺口的变动对通货膨胀的影响程度；参数 决定Phillips曲线的形状。当 时,Phillips曲线恢复为线性形式；当 时,Phillips曲线为非线性的，也就是产出缺口以非线性方式进入Phillips曲线方程中。
Phillips曲线的斜率是参数和 的联合函数，并且随产出缺口 的上升而严格上升：
如果 ，Phillips曲线为凸的；如果 ，Phillips曲线则为凹的。与大部分文献一致，我们采取凸的Phillips曲线（即）。图1给出了这个凸Phillips曲线的一般形式，其中，参数 是一条水平渐近线，它表示超额供给极大时的最大通缩率；我们假设产出缺口的上界为 ，也就是一条垂直渐近线，它表示一种短期约束，即在产出能力达到极限和通胀压力达到极大之前总需求能够增加的产出限度。形如图1的凸Phillips曲线的理论基础是产出能力约束（capacityconstraints），即企业扩大产出的能力是边际递减的，特别是当企业接近产出能力约束的情况下，总需求的增加难以通过提高产出来满足，因而更多地转换为通货膨胀。而当需求降低，特别是超额供给较大时，企业更倾向于积累存货和减少产出，而不是削减价格。
 
y
0
图1凸Phillips曲线
(二)均衡的一阶条件
在新的分析框架下，最优化的目标函数形式虽然保持平方损失函数不变，但由于均衡时的常数通胀目标，使得 。因为 ，加上 为凸函数，其二阶导大于零，由此可导出 。根据 的单调性质可知 。这意味着央行的目标不是最小化 与0的偏差，而是最小化 与0的偏差。基于易处理的目的，我们对式1的时期损失函数进行轻微修改，以 替代 进入损失函数。同时假设总需求曲线不存在不确定性，即假定 ，则 在时期t可以看作前定变量，从而成为时期t的信息集一部分。央行的逐期最小化目标可表示如下：
新的逐期优化问题的一阶条件则为：
由此得到：
把 和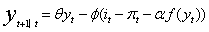 代入上式，可得到新分析框架下的最优货币政策规则：
 (6)
(三)非线性Phillips曲线对货币政策的影响
显然,通过比较线性约束和非线性约束两种情况下的最优利率规则，可以得到如下一些基本结论：
第一，经济结构模型中引入非线性Phillips曲线后，由于式6右边中最后二项的存在，最优货币政策规则也是非线性的。当参数时，式6的非线性最优货币政策规则可以简化式4形式的线性泰勒规则。
第二，在线性泰勒规则下，短期名义利率对通胀边际变化的反应为 。这种情况下，利率的变化是独立于产出缺口和通胀率的，并且对通胀上升和下降的反应是对称的。然而在非线性最优利率规则下，短期名义利率对通胀边际变化的反应为 。与线性规则相对比，在非线性货币政策规则情况下，利率的变化不再是独立的，而是与产出缺口以及通胀与其目标值的偏差相关，并且会产生符号与大小上的非对称。其中，符号上的非对称是指利率对通胀与其目标值的正偏差反应要大于对通胀负偏差的反应；大小上的非对称是指利率并不随通胀的变化而线性的变化。当Phillips曲线为凸的时，利率对通胀变化在符号与大小上的非对称反应主要是因为 关于通胀也是凸函数。这一结论也与Dolado等(2004)的研究相一致。
第三，同样，短期名义利率对产出缺口边际变化的反应也具有类似的结论。当Phillips曲线是线性时，利率关于产出缺口的边际反应为 。 2/3 首页 上一页 1 2 3 下一页 尾页 |
