论文导读::针对一类非线性化程度差别较大的刚性系统,改变以往采用的Newton-Raphson迭代方法,引入Brown算法解决此类非线性刚性系统的数值求解问题。数值试验结果表明,Brown算法对于解决该类问题的有效性。
论文关键词:刚性系统,Brown算法,数值求解
1 引 言
刚性微分方程存在于航空、航天、热核反应、自动控制、电子网络及化学动力学等许多重要科学技术领域及实际问题中[1,2],由于方程的解中既包含有衰减十分迅速的分量,又包含有相对来说变化缓慢的分量,两者的差别可以有好几个数量级,在选定计算方法时带来很大实质困难。实际研究证明,由于数值解稳定性限制,求解刚性微分方程主要采用隐式方法,如:隐式RK方法,BDF方法,IRK方法等。而采用隐式方法将刚性方程离散化以后,其变为线性或非线性方程(组)的求解问题。目前,对线性或非线性方程(组)的求解,多采用Newton-Raphson迭代求解。但对于某些非线性方程组,由于方程之间的非线性化程度相差较大,采用Newton-Raphson迭代方法数值求解的结果并不理想。本文利用Brown算法求解此类非线性刚性系统,具有较高精度和较快迭代速度的优点,数值试验结果表明了该方法的有效性。
2 Brown算法
考虑多个实变量的非线性方程组
 (2.1) (2.1)
的数值求解问题,非线性方程组可以用向量形式表示: ,其中 ,其中 , , 。 。
形如: 的公式称为Newton-Raphson迭代公式。由于该方法是将 的公式称为Newton-Raphson迭代公式。由于该方法是将 , , 同时线性化,所以它并未考虑充分利用 同时线性化,所以它并未考虑充分利用 的具体结构。如果一个非线性的向量函数 的具体结构。如果一个非线性的向量函数 ,其线性精度在各个分量 ,其线性精度在各个分量 , , 上的分布可能是不平衡的,有的分量是非线性函数,而有的分量是线性函数,同时非线性函数组中也有非线性程度高低的差别,在此情况下,利用Newton-Raphson迭代方法对所有分量采用完全相同的数值处理,不利于方法整体计算效率的提高。 上的分布可能是不平衡的,有的分量是非线性函数,而有的分量是线性函数,同时非线性函数组中也有非线性程度高低的差别,在此情况下,利用Newton-Raphson迭代方法对所有分量采用完全相同的数值处理,不利于方法整体计算效率的提高。
针对以上情况,Brown于1969年提出了按分量函数方程 , , 来形成迭代过程[3],其基本思想是对 来形成迭代过程[3],其基本思想是对 各分量 各分量 逐个线性化并用其中每一个线性方程消去余下非线性方程中的一个变量,最后整个方程组就简化为一个仅含单个变量的非线性方程,应用一次单步Newton-Raphson迭代并结合逐一回代,即完成一次迭代过程[4]期刊网。 逐个线性化并用其中每一个线性方程消去余下非线性方程中的一个变量,最后整个方程组就简化为一个仅含单个变量的非线性方程,应用一次单步Newton-Raphson迭代并结合逐一回代,即完成一次迭代过程[4]期刊网。
Brown算法的迭代步骤如下:
第一步,设 为方程组(2.1)解 为方程组(2.1)解 的第 的第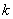 次近似,函数 次近似,函数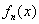 在 在 处近似用线性函数 处近似用线性函数

替代,令 ,由此求出 ,由此求出 : :

定义上式右端为 。 。
第二步,对函数 定义一个新函数 定义一个新函数 Brown算法,且记 Brown算法,且记 ,其中 ,其中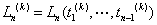 。类似地,用线性函数 。类似地,用线性函数 来近似替代 来近似替代 。令 。令 ,解出 ,解出 , ,
此时, 为 为 个变量 个变量 的线性函数,并记此线性函数为 的线性函数,并记此线性函数为 。 。
第 步,由线性函数 步,由线性函数 ,可得 ,可得 ,利用Newton-Raphson迭代,求得 ,利用Newton-Raphson迭代,求得 ,并由 ,并由 出发,利用 出发,利用 逐一回代,即 逐一回代,即
  (2.2) (2.2)
从而可求出 ,至此完成了一次Brown迭代过程。 ,至此完成了一次Brown迭代过程。
3 数值试验
考虑以下常微分方程组初值问题:
问题1 
其中: ; ; 。 。
问题2
其中: ; ; 。 。
对于上述两问题,当 时,可计算其右函数组的Jacobi矩阵的特征值,均有 时,可计算其右函数组的Jacobi矩阵的特征值,均有 ,其余特征值绝对值均不超过6,因此系统呈强刚性。此外,观察两问题中的右函数组,可以看出除最后一个函数是高度非线性化外,其余函数都是线性的。 ,其余特征值绝对值均不超过6,因此系统呈强刚性。此外,观察两问题中的右函数组,可以看出除最后一个函数是高度非线性化外,其余函数都是线性的。
对于上述两问题,采用隐式Euler方法离散方程组,并分别用Newton-Raphson迭代法与Brown迭代法求解,取步长 ,及相对误差界 ,及相对误差界 ( ( 表示迭代次数)控制每步迭代,最后得到数值解的最大绝对误差界 表示迭代次数)控制每步迭代,最后得到数值解的最大绝对误差界 ,方程真解为:问题1, ,方程真解为:问题1, , , , , ;问题2, ;问题2, , , , , 。计算结果对比分析如表1所示。 。计算结果对比分析如表1所示。
表1 数值计算结果
|

|
问题1
|
问题2
|
|
Newton-Raphson迭代次数
|
迭代18次收敛
|
不收敛,
|
|
Brown迭代次数
|
迭代7次收敛
|
迭代8次收敛
|
|
数值解的绝对误差
(Newton-Raphson迭代)
|
3.83e+001
|
溢出
|
|
数值解的绝对误差
(Brown迭代)
|
1.44e-002
|
3.82e-002
|
4、结束语
对于实际问题中的刚性系统离散化后,如果非线性方程组的线性化程度不同,Brown迭代求解比Newton-Raphson迭代法具有较大的优势,另外需要指出的是在实际运算中,方程应预先进行排列,将线性方程放置在最前,再次为非线性化程度由低到高排列,可以有效的提高运算效率。
参考文献:
[1]李寿佛.刚性微分方程算法理论[M]. 长沙: 湖南科学技术出版社,1997.
[2]刘德贵,费景高.刚性大系统数字仿真方法[M].郑州: 河南科学技术出版社,1994.
[3]Brown,K.M.A Quadratically Convergent Newton-like Method Based on GaussianElimination[J],SIAMJ.Numer.Anal.,1969,(6):560~569.
[4]Van der Houwen,P.J.,Sommeijer,B.P.,Iterated Runge-KuttaMethods on Parallel Computers,SIAMJ.SCI.STAT.COMPUT 12:5(1991):1000~1028
|


