论文导读::由于原状冻土处于自然状态下,其本构关系及水分、温度的分布符合实际状态,而且其实际破坏形式往往是非线性的剪切破坏,所以本文采用了非线性冻土断裂实验模型,对自然状态下的原状冻土进行了断裂破坏实验,着重对Ⅱ型断裂(剪切)破坏的四点弯曲直裂纹试样进行了实验研究。实验过程中改造了四点弯曲实验台,采用着色法测量预制裂纹尺寸。实验原理采用基于能量平衡的方法,利用数据采集系统分别测出了原状冻土四点弯曲试样加力点处位移与力的关系曲线以及相应的非线性参数,推导出裂纹扩展非线性能量释放率计算公式,当试样达到承载极限状况时测试出Ⅱ型断裂试样非线性断裂韧度。同时,提出了修正因子计算非线性断裂韧度的方法,将能量方法测试结果与修正因子方法结果进行了对比,二者基本是一致的。以上提出的冻土Ⅱ型断裂非线性断裂韧度测试方法,及获得的非线性断裂韧度测试结果,为非线性理论研究和工程应用提供了依据。
论文关键词:原状冻土,非线性断裂韧度,实验研究
1.前言
冻土作为地基基础材料,在上部建筑物荷载作用下,其受力破坏的基本形式是剪切破坏[1],其强度准则即为众所周知的莫尔-库仑准则,已被广泛应用在冻土地基基础设计中。近年来在开展常规的强度理论研究的同时,相继开展断裂力学、损伤力学等的研究,其中在断裂力学研究方面取得了长足进展[2~4]。用断裂力学理论研究冻土的剪切破坏,即为冻土材料Ⅱ型断裂问题,它涉及了Ⅱ型断裂强度因子的计算和Ⅱ型断裂韧度的测试问题。冻土材料对温度、内部组织及时间因素的改变非常敏感,是一种性质极不稳定的特殊材料,对金属材料、混凝土材料及岩石等的比较成熟的断裂韧度测试方法[5~7],对冻土材料均不是完全适用的,必须建立考虑冻土特性的测试方法。从冻土工程实际出发,首先应考虑的是冻土非线性特征,其次应考虑冻土在冻结过程中其组构不被破坏,基于以上出发点实验研究,确立了本文的研究宗旨:测定原状冻土在剪力作用的非线性断裂韧度。本文给出了Ⅱ型断裂非线性断裂韧度测试基本原理和方法;进行了原状季节冻土的现场测试;给出了原状冻土Ⅱ型非线性断裂韧度测试结果。为进一步开展冻土非线性理论研究和工程应用提供了依据。
2.冻土非线性断裂韧度测试原理和方法
研究表明,冻土的破坏可分为脆性和塑性性质,在特定的条件下,如低温、高速率以及粗颗粒冻土破坏时呈脆性状态,其特征是应力-应变关系基本是线性的,破坏时有断裂面且有裂纹发展的痕迹并呈严重破碎状,在这种情况,线弹性断裂力学理论是适用的。但是在更一般情况,冻土的破坏通常都是非线性的,这种情况线弹性断裂理论是完全不适用的,必须研究冻土的非线性断裂破坏特征和性质。因此,冻土非线性断裂韧度的测试是研究冻土非线性破坏性质的重要内容之一。
2.1基于能量理论的非线性断裂韧度测试方法
冻土材料在外荷载作用下,冻土中的微裂纹发展并形成微裂纹损伤区,最后形成宏观裂纹,在这个过程中,外力做功为 ,假定它全部转化为材料内的应变能(弹性应变能 ,假定它全部转化为材料内的应变能(弹性应变能 及塑性应变能 及塑性应变能 ),而微裂纹损伤区形成及宏观裂纹形成需消耗能量为 ),而微裂纹损伤区形成及宏观裂纹形成需消耗能量为 ,由贮存的应变能来提供,从能量平衡的角度(无热量损失)则有: ,由贮存的应变能来提供,从能量平衡的角度(无热量损失)则有:
 (1) (1)
当式(1)的能量平衡达到极限状态时:
 (2) (2)
式中  即为非线性能量释放率的临界值,也称为非线性断裂韧度。 即为非线性能量释放率的临界值,也称为非线性断裂韧度。
以Ⅱ型断裂的四点弯曲试样为例(见图3),说明非线性断裂韧度的测试方法期刊网。在加载过程中测试载荷 和加力对应点位移 和加力对应点位移 ,得到 ,得到 曲线,如图1所示。这条曲线的非线性特征可由三个参数来描写: 曲线,如图1所示。这条曲线的非线性特征可由三个参数来描写:
 (3) (3)
式中的 是曲线中直线段的斜率,是裂纹长度 是曲线中直线段的斜率,是裂纹长度 的函数,有: 的函数,有:
 (4) (4)
 , , 是材料常数, 是材料常数, 和 和 ,同样由实验确定。由 ,同样由实验确定。由 曲线可知,当位移达到 曲线可知,当位移达到 时,应变能 时,应变能 (包括弹性、塑性部分)为曲线下的面积,即 (包括弹性、塑性部分)为曲线下的面积,即 实验研究,对任意的 实验研究,对任意的 则有: 则有:
 (5) (5)
将(4)代入(5)式得:
 (6) (6)


将(6)式求导代入(2)式,并考虑到冻土中的微裂纹损伤区刚形成,当不把它作为微裂纹扩展量处理时,外力功 不随裂纹 不随裂纹 变化,则有 变化,则有 ,于是有[8]: ,于是有[8]:
 (7) (7)
当载荷 达到临界值 达到临界值 时,则由上式得到非线性断裂韧度 时,则由上式得到非线性断裂韧度 : :
 (8) (8)
2.2基于修正因子的非线性断裂韧度测试方法
用修正因子法确定非线性断裂韧度可表达为:
 (9) (9)
式中: ――Ⅱ型断裂非线性断裂韧度; ――Ⅱ型断裂非线性断裂韧度;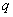 ――非线性修正因子; ――非线性修正因子; ――Ⅱ型断裂的表观断裂韧度,即未考虑非线性影响的断裂韧度。 ――Ⅱ型断裂的表观断裂韧度,即未考虑非线性影响的断裂韧度。
下面分别说明 和 和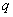 的确定方法。 的确定方法。
(1)表观断裂韧度 的测定 的测定
由四点弯曲试样可知(见图3),在裂纹面的剪切力 ,因此剪应力可求: ,因此剪应力可求:
1/3 1 2 3 下一页 尾页 |


