而表2中三个方程的检验结果表明,第一个方程的拟合效果较好,但第三个方程的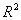 值和F统计量值都较低,这说明 值和F统计量值都较低,这说明 、 、 和 和 量的上一期变化对 量的上一期变化对 本期的总影响是不显著的, 本期的总影响是不显著的, 的变化主要由模型之外的其他变量来决定。然而,在建立VAR模型时一般不根据检验的显著与否来进行变量的筛选,而是保留各个滞后变量。 的变化主要由模型之外的其他变量来决定。然而,在建立VAR模型时一般不根据检验的显著与否来进行变量的筛选,而是保留各个滞后变量。
表1VAR模型参数估计值
|
变量
|
LCY
|
LBY
|
LMC
|
|
LCY(-1)
|
0.849461
|
0.57362
|
-38.70666
|
|
|
(-0.11133)
|
(-0.51281)
|
(-22.271)
|
|
|
[7.62981]
|
[1.11858]
|
[-1.73799]
|
|
LBY(-1)
|
0.09322
|
0.521322
|
43.2754
|
|
|
(-0.08158)
|
(-0.37576)
|
(-16.3189)
|
|
|
[1.14269]
|
[1.38738]
|
[2.65186]
|
|
LMC(-1)
|
0.000476
|
-0.000881
|
-0.417568
|
|
|
(-0.00129)
|
(-0.00596)
|
(-0.25881)
|
|
|
[0.36816]
|
[-0.14776]
|
[-1.61342]
|
|
C
|
0.001087
|
0.048015
|
-8.002995
|
|
|
(-0.0187)
|
(-0.08612)
|
(-3.74023)
|
|
|
[0.05813]
|
[0.55752]
|
[-2.13971]
|
注:表中参数估计值下面的第一个括号内的数字是估计系数
标准差,第二个括号内的数字是t检验统计量值。
表2VAR模型整体检验结果
|
行列式剩余方差(自由度调整)
|
3.47E-06
|
|
行列式剩余方差
|
1.26E-06
|
|
似然函数的对数
|
35.47107
|
|
赤池信息准则
|
-3.353011
|
|
施瓦兹准则
|
-2.805247
|
3.4脉冲响应分析
为了更加清楚地了解 、 、 、 、 这三个变量的动态特征,运用三者的VAR模型,对其进行脉冲响应分析,即计算一个标准差大小的 这三个变量的动态特征,运用三者的VAR模型,对其进行脉冲响应分析,即计算一个标准差大小的 、 、 、 、 冲击分别对 冲击分别对 、 、 和 和 的影响。由此得到脉冲响应表(表4至表6)。 的影响。由此得到脉冲响应表(表4至表6)。
表4LCY的脉冲响应表
|
|
LCY
|
LBY
|
LMC
|
|
1
|
0.013365
|
0
|
0
|
|
2
|
0.013614
|
0.005601
|
0.001192
|
|
3
|
0.013956
|
0.008371
|
0.000309
|
|
4
|
0.013613
|
0.008688
|
0.000446
|
|
5
|
0.013304
|
0.008749
|
0.000338
|
|
6
|
0.012929
|
0.008554
|
0.000346
|
|
7
|
0.01257
|
0.008343
|
0.000325
|
|
8
|
0.012212
|
0.008111
|
0.000318
|
|
9
|
0.011865
|
0.007883
|
0.000308
|
|
10
|
0.011527
|
0.007659
|
0.0003
|
表5LMC的脉冲响应表
|
|
LCY
|
LBY
|
LMC
|
|
1
|
-0.3857
|
0.858321
|
2.502372
|
|
2
|
0.778516
|
2.051813
|
-1.04491
|
|
3
|
0.086021
|
0.150236
|
0.294826
|
|
4
|
0.221195
|
0.31208
|
-0.11539
|
|
5
|
0.139512
|
0.0998
|
0.037645
|
|
6
|
0.151878
|
0.118738
|
-0.00985
|
|
7
|
0.139058
|
0.092848
|
0.007562
|
|
8
|
0.137029
|
0.092983
|
0.001988
|
|
9
|
0.132167
|
0.087837
|
0.003891
|
|
10
|
0.12863
|
0.085683
|
0.003162
|
表6LBY的脉冲响应表
|
|
LCY
|
LBY
|
LMC
|
|
1
|
0.026222
|
0.055695
|
0
|
|
2
|
0.021676
|
0.028279
|
-0.0022
|
|
3
|
0.018424
|
0.016148
|
0.000455
|
|
4
|
0.017534
|
0.013088
|
0.000155
|
|
5
|
0.016755
|
0.011532
|
0.000438
|
|
6
|
0.016243
|
0.010942
|
0.000389
|
|
7
|
0.015751
|
0.010507
|
0.00041
|
|
8
|
0.015299
|
0.010181
|
0.000394
|
|
9
|
0.01486
|
0.009878
|
0.000386
|
|
10
|
0.014436
|
0.009595
|
0.000375
|
由表4-表6可知, 受到自身的脉冲响应要强于 受到自身的脉冲响应要强于 和 和 对它的脉冲响应。对来自 对它的脉冲响应。对来自 和 和 的信息在第一期没有反应。可以看出无论从短期还是长期来说, 的信息在第一期没有反应。可以看出无论从短期还是长期来说, 对自身的冲击皆具有显著、稳定的正向响应; 对自身的冲击皆具有显著、稳定的正向响应; 受其自身的单位冲击具有正向和负向两种响应,在第一期正向最为显著,随后在第2期响应为负,其后稳定在0.003左右。 受其自身的单位冲击具有正向和负向两种响应,在第一期正向最为显著,随后在第2期响应为负,其后稳定在0.003左右。 对来自 对来自 冲击的影响最为显著,长期稳定于0.12,而对于自身的脉冲响应长期趋于0.08; 冲击的影响最为显著,长期稳定于0.12,而对于自身的脉冲响应长期趋于0.08; 对来自 对来自 和自身的冲击的影响都较显著。 和自身的冲击的影响都较显著。 的冲击对 的冲击对 无论短期或长期皆具有正向响应,一直保持下降趋势,稳定于0.014。时滞为2期。 无论短期或长期皆具有正向响应,一直保持下降趋势,稳定于0.014。时滞为2期。
3.5方差分解分析
为了进一步考察三个变量彼此的波动性,利用方差分解技术对 、 、 和 和 各变量的预测均方误差进行分解,并计算出每个变量冲击的相对重要性,方差分解的结果见表7至表9。 各变量的预测均方误差进行分解,并计算出每个变量冲击的相对重要性,方差分解的结果见表7至表9。
表7LCY的方差分解表
|
时期
|
标准差
|
LCY
|
LBY
|
LMC
|
|
1
|
0.013365
|
100
|
0
|
0
|
|
2
|
0.019918
|
91.73534
|
7.906546
|
0.358112
|
|
3
|
0.025723
|
84.43928
|
15.33153
|
0.229191
|
|
4
|
0.030375
|
80.63893
|
19.17518
|
0.185886
|
|
5
|
0.034297
|
78.2972
|
21.54728
|
0.15552
|
|
6
|
0.03764
|
76.8074
|
23.05503
|
0.137572
|
|
7
|
0.040552
|
75.7796
|
24.09544
|
0.124964
|
|
8
|
0.043122
|
75.037
|
24.84704
|
0.115963
|
|
9
|
0.045415
|
74.47648
|
25.41437
|
0.109149
|
|
10
|
0.047478
|
74.03979
|
25.85636
|
0.103849
|
从表7可以看出, 的波动主要受自身冲击的影响,尽管这种影响呈明显的下降趋势,但仍然占74%左右。 的波动主要受自身冲击的影响,尽管这种影响呈明显的下降趋势,但仍然占74%左右。 和 和 的信息对 的信息对 预测方差贡献均在第2步预测时才开始显现, 预测方差贡献均在第2步预测时才开始显现, 的冲击对 的冲击对 的影响非常小;而 的影响非常小;而 的冲击对 的冲击对 的影响则呈上升趋势,长期稳定于25%左右。表明直接融资方式长期对安徽产业结构水平的影响是显著的。 的影响则呈上升趋势,长期稳定于25%左右。表明直接融资方式长期对安徽产业结构水平的影响是显著的。
表8LMC的方差分解表
|
时期
|
标准差
|
LCY
|
LBY
|
LMC
|
|
1
|
2.673452
|
2.081406
|
10.30753
|
87.61107
|
|
2
|
3.613199
|
5.781999
|
37.89026
|
56.32774
|
|
3
|
3.629339
|
5.786864
|
37.72537
|
56.48777
|
|
4
|
3.651265
|
6.08457
|
38.00418
|
55.91125
|
|
5
|
3.655486
|
6.216184
|
37.991
|
55.79281
|
|
6
|
3.660579
|
6.37104
|
37.99057
|
55.63839
|
|
7
|
3.664404
|
6.501756
|
37.97551
|
55.52273
|
|
8
|
3.668144
|
6.628054
|
37.96236
|
55.40958
|
|
9
|
3.671578
|
6.745246
|
37.94863
|
55.30612
|
|
10
|
3.674831
|
6.855831
|
37.93584
|
55.20833
|
从表8可知, 的波动主要受自身冲击的影响,尽管这种影响呈明显的下降趋势,但仍然占55%左右。 的波动主要受自身冲击的影响,尽管这种影响呈明显的下降趋势,但仍然占55%左右。 的冲击对 的冲击对 的预测方差贡献一直处于37%左右。而 的预测方差贡献一直处于37%左右。而 的信息对 的信息对 的影响则处于缓慢增长态势,长期趋于6%左右。说明从长期来看,安徽产业结构水平和间接融资方式对直接融资的影响不容忽视。 的影响则处于缓慢增长态势,长期趋于6%左右。说明从长期来看,安徽产业结构水平和间接融资方式对直接融资的影响不容忽视。
表9LBY的方差分解表
|
时期
|
标准差
|
LCY
|
LBY
|
LMC
|
|
1
|
0.061559
|
18.1446
|
81.8554
|
0
|
|
2
|
0.071161
|
22.85662
|
77.0475
|
0.095883
|
|
3
|
0.075262
|
26.42629
|
73.48434
|
0.089376
|
|
4
|
0.078378
|
29.37148
|
70.54572
|
0.082802
|
|
5
|
0.080975
|
31.7988
|
68.1207
|
0.080503
|
|
6
|
0.083311
|
33.84211
|
66.07965
|
0.078234
|
|
7
|
0.085437
|
35.57805
|
64.34525
|
0.076693
|
|
8
|
0.087392
|
37.06875
|
62.85592
|
0.075331
|
|
9
|
0.089196
|
38.36008
|
61.56573
|
0.074188
|
|
10
|
0.090865
|
39.48767
|
60.43914
|
0.073187
|
表9表明, 的波动主要受自身冲击的影响,尽管这种影响呈明显的下降趋势,但仍然占60%左右。 的波动主要受自身冲击的影响,尽管这种影响呈明显的下降趋势,但仍然占60%左右。 的冲击对 的冲击对 的影响很小;而 的影响很小;而 的冲击对 的冲击对 的影响则呈上升趋势,长期稳定于39%左右,表明产业结构水平间接筹资方式的影响是显著的。 的影响则呈上升趋势,长期稳定于39%左右,表明产业结构水平间接筹资方式的影响是显著的。
4.结论与对策
通过以上实证分析,可以得出以下基本结论及相应对策:
不论长期还是短期,信贷市场和股票市场对安徽产业结构优化均有正向影响,但两者的影响力度有所不同。安徽信贷市场对产业结构的影响长短期均较为显著,且作用时滞为1期;而安徽股票市场对产业结构的影响则相当微弱,作用时滞为1期,其整体作用效果不及信贷市场对产业结构影响的二分之一。
表明,在当前的安徽产业结构优化进程中,直接融资方式仍不能取代间接融资的主体地位,金融机构的贷款仍是企业筹集资金的重要来源;此外,由于目前安徽股票市场的运作还不太规范、结构也不太合理、募集资金使用效率欠佳、政策性风险突出等问题的存在,影响了股票市场直接筹资方式对安徽产业结构优化发展的效用发挥。
同时,安徽产业结构优化的推进对信贷市场和股票市场长期均有显著的正向影响,而且此影响要大于安徽金融结构对产业结构优化的影响程度。尽管安徽产业结构优化对信贷市场的影响短期波动大,发挥作用的时滞长,但却大于其对股票市场的影响。换言之,产业结构优化进程的加快的确是安徽资本市场不断完善的较大推动力,强大的工业实力是资本市场发展壮大的物质基础。
综上所述,一方面,安徽产业结构的优化同样对金融结构的发展完善提供了有力支持,但对股票市场的影响程度大于中长期信贷市场;另一方面,安徽金融结构的发展有力地推进了产业结构优化的进程,但信贷市场的影响力度大于股票市场。 2/3 首页 上一页 1 2 3 下一页 尾页 |


