论文摘要:以球型空腔膨胀理论为基础,提出了一个计算陶瓷靶板阻力的损伤模型,该模型考虑了损伤因子对陶瓷靶板弹道性能的影响。结合不可压缩流体力学理论,对射流侵彻陶瓷靶板的侵彻速度进行了理论值计算,并与未考虑损伤的侵彻速度进行了比较,该模型的计算结果更接近实验结果。建立了射流侵彻陶瓷靶板的数值计算模型,对铜射流侵彻陶瓷靶的动态破坏过程进行了研究,讨论了药型罩的锥角、壁厚对射流侵彻结果的影响,结果表明:相同锥角的药型罩,壁厚对陶瓷靶板孔径的影响较小;同壁厚的药型罩,随着锥角的增大,侵彻孔径增大。侵彻速度的数值模拟结果与理论结果进行了比较,得到了较好的一致性。
论文关键词:射流,空腔膨胀模型,损伤,数值模拟,陶瓷
引言
很多材料都可以替代钢板作为抗动能弹侵彻和射流侵彻的装甲组件,其中AlO,AlN和TiB等陶瓷材料以其高强度、高硬度、耐磨、耐腐蚀和密度小等特点,广泛的应用于装甲防护中。但是陶瓷材料的抗侵彻机理仍然不是十分清楚,因此世界各地的研究学者纷纷对陶瓷的弹道性能进行了研究。通常,靶板阻力被用来衡量陶瓷靶板的抗侵彻能力,而人们较多的利用空腔膨胀模型结合一定的材料模型来分析陶瓷靶侵彻/穿甲的侵彻阻力。Tate提出了一个理论模型,认为靶板阻力是材料的动态屈服强度;Sternberg认为靶板阻力是使球型空腔半径从零开始增加所需要的准静态压力;Forrestal和Longcope根据空腔膨胀理论得到了靶板阻力的表达式。Satapathy和Bless、Forrestal和Longcope将准静态空腔膨胀理论推广到陶瓷材料的靶板阻力计算中。Satapathy假设空腔膨胀的速度是一定的,并用动态空腔膨胀理论求得了陶瓷材料的靶板阻力。
对于射流侵彻陶瓷靶板过程的数值模拟,较一般的方法是利用Johnson-Holmquist本构模型,分别描述完善材料和粉碎区失效材料的压缩强度,损伤数D定义为应变函数,在0(完善)和1(粉碎)之间变化。最常用的数值模拟射流侵彻陶瓷靶板的软件有:有限差分方法软件AUTODYN和有限元软件LS-DYNA。张先锋等用LS-DYNA模拟了射流侵彻陶瓷靶板的过程,并研究了盖板约束对陶瓷靶板抗射流侵彻的影响。黄正祥等用LS-DYNA对射流侵彻不同倾角的陶瓷复合靶板进行了数值模拟,分析了倾角对陶瓷抗射流侵彻能力的影响。张晓晴、韩永要等人用LS-DYNA对陶瓷靶板抗动能弹侵彻的过程进行了数值模拟。石广玉、MasahideKatayama等人用AUTODYN对射流形成进行了数值模拟。
本文在准静态空腔膨胀理论的基础上,考虑了陶瓷材料的损伤,建立了计算陶瓷材料抗射流侵彻靶板阻力的损伤模型,结合不可压缩流体力学理论预测了射流的侵彻速度。利用软件模拟了射流侵彻AD995陶瓷靶板的动态过程,得到了陶瓷靶板的损伤状态、侵彻孔径和侵彻速度等结果,讨论了药型罩壁厚、角度对侵彻结果的影响。
2陶瓷靶板抗射流侵彻的理论模型
2.1考虑靶板强度的不可压缩流体力学理论
高速射流侵彻靶板的定常不可压缩流体力学理论,其基本关系是Bernoulli方程。实验表明靶板的强度对破甲过程有很大影响,特别是射流速度较低时,不能忽略靶板的强度。加入靶板强度项的伯努利方程可以表示为
 (1) (1)
其中, 和 和 分别为射流和靶板的材料密度; 分别为射流和靶板的材料密度; 和 和 分别为射流速度和侵彻速度(射流和靶板的接触面速度);R为靶板阻力,是一个强度参数。求解方程(1),可得侵彻速度 分别为射流速度和侵彻速度(射流和靶板的接触面速度);R为靶板阻力,是一个强度参数。求解方程(1),可得侵彻速度
 (2) (2)
2.2考虑损伤的空腔膨胀模型
为了求得侵彻速度,需要对方程(2)中的R进行求解。冲击载荷下的氧化铝的破坏特征,如图1所示。根据氧化铝陶瓷在冲击载荷下的破坏状态,半无限大的陶瓷靶板可以被分为如图2的五个不同的区域:空腔区、粉碎区,径向裂纹区,弹性区和未响应区。
 
图1陶瓷受冲击后的损伤特征图图2靶体响应区
Fig.1DamagecharacteristicsofceramicunderimpactFig.2Responseregionsinthetarget
根据陶瓷靶板的受力特点及抗压强度大于抗拉强度等力学特性,陶瓷响应区的边界条件可以写为(本文假设拉应力为正,压应力为负):
 (弹性区和未响应区的边界处,无应力); (弹性区和未响应区的边界处,无应力);
 (当环向应力达到陶瓷材料的拉伸强度时,材料产生径向裂纹); (当环向应力达到陶瓷材料的拉伸强度时,材料产生径向裂纹);
 (当径向裂纹区的径向应力达到陶瓷材料的压缩强度时,发生破碎)。 (当径向裂纹区的径向应力达到陶瓷材料的压缩强度时,发生破碎)。
其中 为半径; 为半径; 、 、 、 、 和 和 分别为空腔区、粉碎区、径向裂纹区和弹性区的外半径; 分别为空腔区、粉碎区、径向裂纹区和弹性区的外半径; 为径向应力; 为径向应力; 为环向应力; 为环向应力; 为陶瓷材料的单轴拉伸强度; 为陶瓷材料的单轴拉伸强度; 为材料的单轴压缩强度。 为材料的单轴压缩强度。
本文的损伤模型以传统的准静态空腔膨胀模型为基础,假设径向裂纹区的材料在径向亦存在损伤,并提出损伤因子形式如下:
 (3) (3)
该损伤因子满足
 (4) (4)
应力表达式为
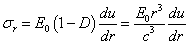 (5) (5)
根据传统空腔膨胀模型理论,可以求得考虑损伤的半无限靶板的靶板阻力为
 (6) (6)
其中 , , 为材料的压减系数; 为材料的压减系数; 是泊松比; 是泊松比; 为初始弹性模量。 为初始弹性模量。
一般来说,在小炸高条件下,对于简单的锥形或半球形药型罩来说,大部分侵彻模型假定射流速度在空间分布是线性的。根据射流侵彻靶板的实验,假设射流在未侵彻时,沿射流长度方向线性变化,射流着靶速度 ,侵彻速度 ,侵彻速度 。陶瓷材料参数: 。陶瓷材料参数: , , , , , , , , , , , , 。 。 1/3 1 2 3 下一页 尾页 |


