论文摘要:本文结合实例分析了马尔柯夫模型在市场占有率中的应用。作者首先对马尔柯夫模型的基本理论进行详细的介绍,重点分析了该方法计算过程中的三个主要步骤。在此基础上,作者基于马尔柯夫模型,对三个销售复合肥的农资超市的市场占有率进行了预测。
论文关键词:马尔柯夫模型,市场占有率,农资,复合肥市场
一、问题的提出
前段时间,我们对广西荔浦县农资经营情况进行了调查。当地一群众在农业产业化发展的关键时期,敢于创新,积极引进现代营销方式,建立农资超市,主要销售化肥、农药等农资产品,方便了广大农户,获得了较好的经济效益。
同时,我们也发现,在当地的农资经超市许多经销商销售手段同质化严重,规模大小相似,造成竞争日益加剧。因此,从某个农资超市的微观角度出发,去预测未来一定时期的市场占有率,特别他们在某个区域的市场占有率,就具有很强的现实意义。这样有利于他们知彼知己,以制定科学有效的市场营销策略。
本文将以广西荔浦县的M镇复合肥销售为例,根据它们的历史顾客数量,假如在未来的时间内,在其它促销手段和宏观环境等不变的情况下,预测各个农资超市复合肥的市场占有率。
通过这一实例,将使读者对马尔柯夫在市场预测中的应用有一个比较系统的了解,从而把马尔柯夫预测应用到其他产品领域的市场预测中去,为企业发展服务。
二、关于马尔柯夫模型
马尔柯夫预测以俄国数学家A.A.Markov名字命名,是利用状态之间转移概率矩阵预测事件发生的状态及其发展变化趋势,也是一种随时间序列分析法。它基于马尔柯夫链,根据事件的目前状况预测其将来各个时刻(或时期)的变动状况。
在这里,我们将主要介绍和分析马尔柯夫链,转移矩阵和马尔柯夫预测步骤三个问题。
(一)马尔柯夫链
设预测对象为一系统,若该系统在某一时刻可能出现的状态为Ei,而该系统从状态Ei变化到另一状态Ej的状态转移过程称为马尔柯夫过程。一个马尔柯夫过程若具有如下的两个特征,则称其为马尔柯夫链。
一是具有无后效性。即系统的第n次试验结果出现的状态,只于第n-1次时所处的状态有关,与它以前所处的状态无关;
二是具有稳定性。即在较长时间下,该过程逐渐趋于稳定状态,而与初始状态无关
(二)转移矩阵
系统由状态Ei经过一次转移到状态Ej的概率为pij,则系统全部一次转移概率的集合所组成的矩阵称为一次转移矩阵,记为:
K次转移矩阵记为P(k)
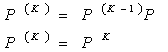 转移矩阵具有以下两个性质: 转移矩阵具有以下两个性质:
(三)马尔柯夫预测步骤
设系统在K=0时所处的初始状态为已知,即初始状态向量
 S= S=
经过K次转移后所处的状态向量记为:

满足以下条件,当:

把它写为矩阵形式为:
 当系统处于稳定状态时, 当系统处于稳定状态时,
所以:


三、举例:M镇复合肥市场占有率预测
复合肥销售旺季每年的3月和4月,主要用于给水稻、荔浦芋、甘蔗和椪柑的施肥。M镇共有3家农资超市,分别是良农农资超市,阿满农资超市和金丰农资超市。我们调查知道,2009年3月和2010年3月三家农资超市的复合肥的销售量,每个农户3月购买复合肥的数量平均是2.7包。为使计算方便,我们以购买的农户数量为市场占有率的计算标准。根据马尔柯夫模型的特点,我们假设购买复合肥的农户数量和他们每家购买复合肥的包数在计算期内保持不变,他们选择的商家以这3个农资超市为范围。这样,我们将通过马尔柯夫模型预测各个超市在未来若干年的场占有率。
三家农资超市具体的情况如下:2009年3月有1500人到良农农资超市购买复合肥,有1500到阿满农资超市购买复合肥的有,而到金丰农资超市有2000人。
2010年3月,由于各种原因,购买复合肥的农户流动发生了以下变化:
1、良农农资超市在2010年3月有1200人继续保留在本店购买复合肥,转移到心阿满农资超市购买的有100人,转移到金丰农资超市购买的有200人。
2、阿满农资超市在2010年3月有1000人继续保留在本店购买复合肥,转移到良农农资超市购买的有200人,转移到金丰农资超市购买的有300人。
3、金丰农资超市在2010年3月有1500人继续保留在在本店购买复合肥,转移到良农农资超市购买的有的有200人,转移到阿满农资超市购买的有300人。
转移状况如表1所示。
通过马尔柯夫模型,我们可以预测2010年3月和2011年3月以及稳定状态下的市场占有率。
表1:2010年3月观众转移转移状况
|
到
从
|
良农农资超市
|
阿满农资超市
|
金丰农资超市
|
合计
|
|
良农农资超市
|
1200
|
100
|
200
|
1500
|
|
阿满农资超市
|
200
|
1000
|
300
|
1500
|
|
金丰农资超市
|
300
|
200
|
1500
|
2000
|
求解过程如下
(一)根据调查资料,确定初始状态概率向量为:

下标:
1:良农农资超市2:阿满农资超市3:金丰农资超市
计算它们的转移矩阵:
(二)根据公式,我们可以计算2010年3月和2011年3月的三个超市的市场占有率。
 2010年3月三个超市的复合肥市场占有率: 2010年3月三个超市的复合肥市场占有率:
所以,2010年3月三个超市的复合肥市场占有率分别为:0.34,0.26,0.4
同理得2011年3月的市场占有率;
所以,2011年3月三个超市的复合肥市场占有率:0.367,0.236,0.397
(三)求稳定状态下三个超市复合肥的市场占有率:
 根据公式: 根据公式:

从计算结果可以看出,经过N期转移,三个超市的复合肥市场占有率达到稳定,他们的市场占有率分别是42%,20%,38%。 1/2 1 2 下一页 尾页 |


