论文摘要:斜抛运动最大射程问题的研究-论文网
论文关键词:运动,最大,射程,问题,研究
在山东科学技术出版社出版的普通高中课程标准实验教科书《物理2》(必修)的第3章第4节“斜抛运动”中的“信息窗”栏目“铅球出手时的仰角应该是45吗?”中说:
把在某一水平面的某物体以一定的初速度(v)斜向上抛出,如果空气阻力可以忽略,则它落回同一水平面时,其水平位移(即射程)以仰角为45时最大。但是,推铅球时抛掷点不在地面上,而是离地面有一高度h,以大小相同的初速度分别按45及40仰角抛掷,当落回到抛掷点所在平面时,水平位移以45的较大。但是,当落到地面时,水平位移却以40时较大。
教科书没有说明为什么,本文进一步研究这个问题。
设铅球被抛出的初速度为 ,抛射角(即初速度方向与水平面的夹角)或仰角为 ,抛射角(即初速度方向与水平面的夹角)或仰角为 ,则 ,则
1.落回同一水平面时。
则根据运动的分解,
水平方向: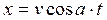 (1) (1)
竖直方向: (2) (2)
当 时,物体落回同一水平面,令(2)式为0,得 时,物体落回同一水平面,令(2)式为0,得
 (3) (3)
将(3)代入(1)得: (4) (4)
根据三角知识,当 时, 时, 取最大值,为 取最大值,为 。 。
2.落在抛掷点以下时,
设落点在抛点以下 处,令(2)式中 处,令(2)式中 ,即 ,即
  = = ,解得 ,解得
  (5)根据物理意义式中取“+”号, (5)根据物理意义式中取“+”号,
将(5)代入(1)式得
  (6) (6)
求(6)式极值,几乎是不可能的。猜想: 与h、v有关。 与h、v有关。
2.1初速度 (设为10 (设为10 )相同时 )相同时
我用电脑的Excel列表画图,表省略,图如下。
 从图、表可以看出,当 从图、表可以看出,当 时,两图象相交,其物理意义是:在落点在抛点以下 时,两图象相交,其物理意义是:在落点在抛点以下 以内,以仰角为45时,其水平位移(即射程)最大。在落点在抛点以下 以内,以仰角为45时,其水平位移(即射程)最大。在落点在抛点以下 以外,以仰角为40时,其水平位移(即射程)较大。 以外,以仰角为40时,其水平位移(即射程)较大。
那么,是不是以仰角为40时,其水平位移(即射程)最大呢?笔者进行了进一步的研究,把仰角分别为37、40、43、45、48等5种情况分别求出对应的 、 、 值并在同一坐标图中作图,结果如下: 值并在同一坐标图中作图,结果如下:
 从图、表可以看出,图象的交点不在一起,其物理意义是:在不同的落点范围,对应于最大射程的抛射角是不同的。例如在 从图、表可以看出,图象的交点不在一起,其物理意义是:在不同的落点范围,对应于最大射程的抛射角是不同的。例如在 左右,以仰角为40时,其水平位移(即射程)最大,当在 左右,以仰角为40时,其水平位移(即射程)最大,当在 左右,以仰角为37时,其水平位移(即射程)最大。 左右,以仰角为37时,其水平位移(即射程)最大。
2.2设初速度为 时,抛射角分别为40和45的图象如下 时,抛射角分别为40和45的图象如下
 从图、表可以看出,两图象的交点为 从图、表可以看出,两图象的交点为 ,其物理意义是:在落点在抛点以下 ,其物理意义是:在落点在抛点以下 以内,以仰角为45时,其水平位移(即射程)最大。在落点在抛点以下 以内,以仰角为45时,其水平位移(即射程)最大。在落点在抛点以下 以外,以仰角为40时,其水平位移(即射程)较大。 以外,以仰角为40时,其水平位移(即射程)较大。
与2.1比较可以得到:不同的初速度,即使落点在相同的高度(都在抛点以下),对应于最大射程的抛射角,也是不同的。例如,对于 高的人来说,如果初速度为10m/s,他用40的抛射角抛得最远,如果初速度为20m/s,他用45的抛射角抛得最远。 高的人来说,如果初速度为10m/s,他用40的抛射角抛得最远,如果初速度为20m/s,他用45的抛射角抛得最远。
总结:斜抛运动中,抛射体落在抛点水平面以下,是不是40时射程最大,与抛点离地面的高度h有关,也与初速度 的大小有关。 的大小有关。 |


