40岁以下年龄段的职工数为 ,则应抽取的人数为 ,则应抽取的人数为 人. 人.
分析:要特别注意系统抽样与分层抽样的区别与联系.系统抽样要求将总体均衡的分成几个部分,从每部分中抽取相同个数的样本;分层抽样要求各层有明显的差异,在每一层中按比例抽取个体.
五、条形图与直方图
条形图和直方图,都是用来表示试验结果(即随机变量)的频率分布情况的图形.如果随机变量是离散型的,就可以用高度来表示各个随机变量取值的频率(或频数).其图形是相互分离的矩形.相应的图形就是频率分布条形图.
18.(2007高考北京理)某中学号召学生在今年春节期间至少参加一次社会公益活动(以下简称活动).该校合唱团共有100名学生,他们参加活动的次数统计如图所示.(条形图)
(I)求合唱团学生参加活动的人均次数;
(II)从合唱团中任意选两名学生,求他们参加活动次数恰好相等的概率.
(III)从合唱团中任选两名学生,用 表示这两人参加活动次数之差的绝对值,求随机变量 表示这两人参加活动次数之差的绝对值,求随机变量 的分布列及数学期望 的分布列及数学期望 . .
解:由图可知,参加活动1次、2次和3次的学生人数分别为10、50和40.
(I)人均次数为: . .
(II)选出的两名学生,参加活动次数恰好相等的概率为 . .
(III)  ; ;  ; ;
 的分布列: 的分布列:
 的数学期望: 的数学期望: . .
如果随机变量是连续型的,就把随机变量所在的区间分成若干等份,每等份称为一组,用组矩表示每个矩形的宽,用频率与组矩的比表示矩形的高,就可以得到一些互相连在一起的矩形.这样的图形就是频率分布直方图.
例如.(2009山东卷理)某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的   产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是() 产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是()
A.90 B.75 C. 60 D.45
【解析】:产品净重小于100克的概率为(0.050+0.100)×2=0.300, 
已知样本中产品净重小于100克的个数是36,设样本容量为 , ,
则 ,所以 ,所以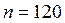 ,净重大于或等于98克并且小于 ,净重大于或等于98克并且小于
104克的产品的概率为(0.100+0.150+0.125)×2=0.75,所以样本
中净重大于或等于98克并且小于104克的产品的个数是
120×0.75=90.故选A.
六、正态分布 与标准正态分布 与标准正态分布
设某个总体的期望是 ,标准差 ,标准差 .就把随机变量 .就把随机变量 的概率函数 的概率函数  叫做正态函数,其分布叫做正态分布,记作 叫做正态函数,其分布叫做正态分布,记作 ~ ~ , , 的图象叫做正态曲线. 的图象叫做正态曲线.
特别,当 , , 时,相应的函数可化为 时,相应的函数可化为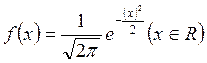 .这就是标准正态函数,其分布叫做标准正态分布,记作 .这就是标准正态函数,其分布叫做标准正态分布,记作 ~ ~ . .
在正态分布 ~ ~ 中,用F 中,用F 表示随机变量 表示随机变量 的概率,即F 的概率,即F = = ;在标准正态分布 ;在标准正态分布 ~ ~ 中,用Φ 中,用Φ 表示随机变量 表示随机变量 的概率,即Φ 的概率,即Φ = = .两者之间的换算关系是 .两者之间的换算关系是 =Φ =Φ . .
例如,(2007年高考安微,10)以 表示标准正态总体在区间 表示标准正态总体在区间 内取值的概率,若随机变量 内取值的概率,若随机变量 服从正态分布 服从正态分布 ,则概率 ,则概率 等于() 等于()
A. B. B. C. C. D. D.
分析:∵ = = = =
= =Φ =Φ —Φ —Φ
=Φ —Φ —Φ .∴选B. .∴选B.
2/2 首页 上一页 1 2 |


