证明数列不等式的常用方法
论文关键词:数列不等式
数列不等式数列是含有数列的通项或前n项和的不等式.在近年来的高考数学试题中,经常会见到关于数列不等式的证明问题.而数列不等式的证明大多数都是比较麻烦的.
由于数列不等式都是与自然数n有关的不等式.所以在证明数列不等式时,人们最先想到的是利用数学归纳法.但是,只用数学归纳法,并不能完全解决数列不等式的证明问题.
例如,对于不等式 .如果用数学归纳法证明,则过程如下下: .如果用数学归纳法证明,则过程如下下:
(1)当 时,左 时,左 ,右 ,右 ,不等式成立. ,不等式成立.
(2)假设 时,不等式成立.即 时,不等式成立.即 . .
 时,对上式两端同时加上 时,对上式两端同时加上 ,可得 ,可得

下面只需证 成立,此式等价于 成立,此式等价于 ,因为这个式子的分母为正数,所以可等价转化为 ,因为这个式子的分母为正数,所以可等价转化为 ,由此得 ,由此得 .这显然是矛盾的.这说明利用数学归纳法,是不能证明这个不等式的.对这个不等式,在后面的例题1中进行证明. .这显然是矛盾的.这说明利用数学归纳法,是不能证明这个不等式的.对这个不等式,在后面的例题1中进行证明.
对于数列不等式的证明,需要利用各种方法,其中放缩法最为重要.应该把放缩法与数学归纳法、比较法、分析法等各种方法结合起来使用;还可以构造函数,利用函数的单调性及最值进行证明.在具体证明过程中,需要根据题目的实际情况,选择适当方法.只有巧妙地把各种方法结合起来,才能够较好地解决数列不等式的证明问题.下面介绍几种证明数列不等式的常用方法,供大
参考.
一、根据题目的特征适度放缩,用放缩法证明数列不等式
例1 在数列 中, 中, 为其前n项和,且满足 为其前n项和,且满足 . .
(1)求数列 的通项公式; 的通项公式;
(2)证明: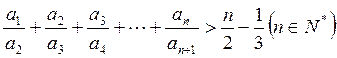 . .
 解:(1)∵ 解:(1)∵  , ,
∴  , ,  . .
又 , , .∴ .∴  . .
(2)∵  , ,
∴  ,把这 ,把这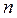 个不等式相加可得 个不等式相加可得
  . .
【评析】:本题证明的关键,是根据数列不等式的特征,分离出需要的常数,得到不等式 .再把这 .再把这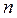 个不等式相加,并用等比数列求和公式化简,然后用放缩法证明. 个不等式相加,并用等比数列求和公式化简,然后用放缩法证明.
二、先用数学归纳法猜想并证明通项公式,再用放缩法证明
例2 (2008年高考辽宁)在数列 , , 中, 中, , , ,且 ,且 , , , , 成等差数列, 成等差数列, , , , , 成等比数列( 成等比数列( ). ).
(Ⅰ)求 , , , , 及 及 , , , , ,由此猜测 ,由此猜测 , , 的通项公式,并证明你的结论; 的通项公式,并证明你的结论;
(Ⅱ)证明: . .
解:(Ⅰ)由条件得 由此可得 由此可得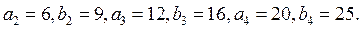
猜测 下面用数学归纳法证明: 下面用数学归纳法证明:
①当n=1时,由 , , ,可知结论成立. ,可知结论成立.
②假设当n=k时,结论成立,即
那么当n=k+1时, , ,
所以当n=k+1时,结论也成立.
由①②,可知 对一切正整数都成立. 对一切正整数都成立.
(Ⅱ) n≥2时,由(Ⅰ)知 n≥2时,由(Ⅰ)知
故
=
= 综上,原不等式成立. 综上,原不等式成立.
【评析】:这个题的证明过程中,“ ”是最关键的一步,通过这一步的放缩,就可以进行下一步的拆项相消了. ”是最关键的一步,通过这一步的放缩,就可以进行下一步的拆项相消了.
三、在用数学归纳法证明的第二步过程中,利用放缩法进行证明
例3.(2009年高考山东)设等比数列{ }的前n项和为 }的前n项和为 ,已知对任意的 ,已知对任意的 , ,
点 ,均在函数 ,均在函数 且 且 均为常数)的图像上. 均为常数)的图像上.
(Ⅰ)求r的值;Ⅱ)当b=2时,记  ,m ,m
 求证:对任意的 求证:对任意的 ,不等式 ,不等式 成立. 成立.
解:(Ⅰ)因为 ,所以当 ,所以当 时, 时, , ,
当 时, 时, , ,
又因为{ }为等比数列, }为等比数列, , ,
所以, ,并且 ,并且 . .
(Ⅱ)当b=2时,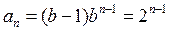 , ,
则 ,所以 ,所以 w.w.w.,,,k.s.5.u.c.o.m , w.w.w.,,,k.s.5.u.c.o.m ,
因此,只需证明不等式  成立.因为 成立.因为
①当 时,左边= 时,左边= ,右边= ,右边= ,因为 ,因为 ,所以不等式成立. ,所以不等式成立.
②假设当 时不等式成立,即 时不等式成立,即 成立. 成立.
则当 时,左边为 时,左边为
    . .
 所以,当 所以,当 时,不等式也成立. 时,不等式也成立.   由①、②可得不等式 由①、②可得不等式 恒成立.所以要证的原不等式也成立. 恒成立.所以要证的原不等式也成立.
【评析】本题主要考查等比数列的定义、通项公式、求和公式以及数列不式的证明.在证明过程中,利用了数学归纳法和放缩法.其中,用均值不等式缩小是最关键的一步.
四、在用放缩法证明的同时,构造函数并用其单调性证明数列不等式
例4 (2009年高考广东)   已知曲线 已知曲线 .从点 .从点 向曲线 向曲线 引斜率为 引斜率为 的切线 的切线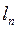 ,切点为 ,切点为 . .
(1)求数列 的通项公式; 的通项公式;
(2)证明: . .
解:(1)可设切线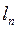 为 为 ,联立 ,联立 得 得 ,则 ,则 , ,
∴ ( ( 舍去),由此解得 舍去),由此解得
 , , . .
 (2)证明:∵ (2)证明:∵ w.w12二 w.w12二  , ,
.
∴ . .
由于 ,可令函数 ,可令函数 ,则 ,则 ,令 ,令 ,得 ,得 .在区间 .在区间 上, 上, ,则 ,则
函数 在 在 上单调递减.∴ 上单调递减.∴ ,即 ,即 在 在 恒成立, 恒成立,
又 ,则有 ,则有 ,即 ,即 . .   w.w.w.k.s. w.w.w.k.s. 【评析】前面的放大过程中是利用不等式 【评析】前面的放大过程中是利用不等式 : : ,由此得 ,由此得 . .
五、利用作差、作商比较法或者分析法,也可以证明数列不等式
例5(2009年高考安微)已知数列{ }的 }的
1/2 1 2 下一页 尾页 |


