对五年制大专学生数学教学的思考

【摘要】初中毕业进入五年制大专学习的学生，要在两年的时间里学完高中的所有课程，三年的时间里学完大学本科的所有基本课程，任务十分艰巨。由于数学的连贯性很强，对于数学基础较差的学生来说，教师应如何实施对他们的数学教学，使他们能顺利完成五年的数学学习，本文从四个方面谈了一下自己的观点。
论文关键词：五年制大专,数学教学,多媒体辅助教学,选修课

我从事五年制大专数学教学以来，经历了每一个年级的许多数学课程。在此过程中，发现了不同阶段的优秀学生的许多不同特点，尤其是对待学习的态度和学习方法的不同。针对他们的特点和实际情况，我总结出如下几点对五年制大专学生的数学教学方法，望与大家共享。

一．基础阶段培养学习习惯和方法是关键

五年制大专学校招收的五年制大专学生都是初中毕业没有考上高中的学生，他们的基础知识较差，其主要原因就是在小学和初中阶段由于自身，学校和家长等原因，没有养成良好的学习习惯和学习方法，他们要么眼高手低，粗枝大叶，要么苦学，死学，尤其对数学的学习，没有良好习惯，方法，使得他们在初二到初三拉开距离。针对上述特点，教师在对一年级新生上课，一开始就要以“严”字开头，在详细回顾以前知识的基础上，认真细致的讲解现在的知识，注重提问和学生板演并及时对学生回答问题的方式，板演和作业中的格式，计算过程进行强调，从一开始就严格要求。另外，他们的模仿能力还很强，教室上课的态度也十分重要，上课时，千万不要因为某些内容计算繁琐，费时而一带而过，不去演示。如某些函数定义域，值域的求解过程，要解很复杂的不等式组，教师就应详细去解，这样一方面可以回顾不等式的解法，另一方面可以培养学生的耐心认真仔细的学习习惯和学习态度，使得他们在以后的学习中不轻易放弃；再比如在《概率与统计》里，某些概率公式的推导过程，问题的求解过程及用计算器求方差，标准差，平均数的过程教师也不应采取“蜻蜓点水”式，而应同学生一起动手，这样既可以增进师生感情又可以培养学生善于思考，勤于动手的习惯，有助于他们形成自己的一套良好的学习方法。

二．理清脉络是提高阶段增强学生自信的有效措施

基础阶段主要学习的是高中的一些知识，教师在上课时就可以在复习回顾相关初中知识的基础上，使得大专一，二年级的学生能很轻松自如的掌握，尤其是大专一二年级数学教材，他将高中数学及部分大学本科一年级数学知识分成很小的知识系统而只介绍每个系统中比较浅显的内容，知识量少，时间多，加上教师详细讲解十分易被接受。而进入大专三年级以后，数学教育专业加入了大学本科数学系的专业课《数学分析》《高等代数》《空间解析几何》等其难度也和本科数学系的专业课相当，对于没有经历三年高中磨练，没有高考压力的他们来说，在两年之后的知识水平自然较高中毕业，考上大学的学生相比差的较远，因而，教师就应采取“简单化”的方式，旨在理清教材中诸多定义，定理的含义及证明脉络，主要通过例题使学生学会应用定义，定理解决相关问题即可，这样既可以是学生理解了所学知识，为继续学习打下基础又可以增强学生的自信心。

例如，对数列或函数极限迫敛性的证明就可以简单化。以函数极限的迫敛性为例:

对于三个函数f(x),g(x),h(x),如果满足

（1）在x0的某个邻域内恒有f(x)≤g(x)≤h(x)

（2）

则

教师可如此说明：

再如对《高等代数》的“克莱姆”法则来说，也只需着重介绍其作用，应用时应注意的问题，简单介绍其证明的依据，概括的理清证明的方法即可。否则按照教材内容按部就班得讲证明过程，既费时又易使学生忽略法则本身的重要性，而且由于其难度较大，大部分学生听不懂，既分散学生的注意力又可能使他们感到该门课程难度太大而失去学习的勇气。

三．多媒体辅助教学的有效性

（1）节省时间

首先，大专数学课程中许多定义，定理内容本身就很长，教师如不让这些内容在黑板上出现不利于分析，若出现，要写在黑板上有很费时间且在写的这段时间里，易使教室气氛冷清，不利于学生学习热情的继续，这时，多媒体教学则十分可取。例如反函数的定义：

对于函数,设它的定义域是A,值域是C,根据中x和y的关系，用y表示出x，

得到，对于C中的任意一个值都有为以确定的x和它对应，则称为的反函数，记作，习惯上写为。

如将这段话写在黑板上，则显然费时，不写则不利于分析定义并有定义找到求反函数的方法，这时如采用多媒体事先写好，上课时只需放映，教师则可在黑板上将上述定义写出主要内容：

C 函数

C 函数

函数

它利于学生理解，消化，吸收和应用。诸如此类例子在《数学分析》《高等代数》中更是举不胜举，几乎每章每节的定义，定理都适用多媒体教学，他完全可以贯穿数学教学的整个过程中。

其次，在通过例题得出某一结论或做题方法需要向学生点明而有不便与写时，或课时总结时，多媒体教学又会给我们带来方便和效率。

例如，教师在讲完求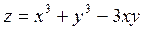的极值这一例题后就可放映出幻灯片：

1.求稳定点P(a,b);

2.求稳定点处二阶偏导数:A=a,b),

3.判断

4.计算极值。

然后在对照上述四步回顾例题，可是学生形成一套做这一类题目的方法且放映幻灯片给学生节省了记忆，理解和消化的时间。

（2）图示效应

在解析几何和数学分析中有许多图形教师若在黑板上画出来，既费时又不利于切割，旋转，为使学生可以真切的观察特点，总结结论，而利用多媒体教学手段，则可得到意想不到的效果。

例：

由得(0,0)是的稳定点；

由A=,=0-2*（-2）=4>0

得（0,0）不是的极值点。

整个做题过程抽象，难理解，若由多媒体辅助手段生成的图象，给出图示，则十分清楚，极易于理解，并很快就会得出结论：极值点不一定是稳定点。并由于图像的出现，学生记忆深刻。

再例如:在给出求可微函数极值步骤中有一点：=0时，稳定点

不确定是极值点，还是不是极值点，学生不易理解，此时若用多媒体生成

的图象，给出图示分析则很快就会得出结论：当=0时，稳定点可能是也可能不是极值点。

 1/2    1 2 下一页 尾页