而且,Eviews给出了分布滞后模型中诸 的估计值。这些系数估计值分别为0.5165、0.5756、0.1775,分别表示制度因素x10增加一个单位,在当期将使农业总产值y增加0.5165个单位;由于存在时间滞后的影响,x10增加一单位还将在下一期使得农业总产值y增加0.5756个单位;在第二期则使得农业总产值y增加0.1775个单位。 的估计值。这些系数估计值分别为0.5165、0.5756、0.1775,分别表示制度因素x10增加一个单位,在当期将使农业总产值y增加0.5165个单位;由于存在时间滞后的影响,x10增加一单位还将在下一期使得农业总产值y增加0.5756个单位;在第二期则使得农业总产值y增加0.1775个单位。
图2所示的估计结果的最后一行SumofLags是诸 系数估计值的总和,其反映的是分布滞后变量x10对因变量y的长期影响(即长期乘数),即从长期看,x10增加一个单位将使得y增加1.2696个单位。 系数估计值的总和,其反映的是分布滞后变量x10对因变量y的长期影响(即长期乘数),即从长期看,x10增加一个单位将使得y增加1.2696个单位。
同上分析,可得以下结果:人力资本投入对贵州省农业经济增长的影响滞后三年左右,且人均人力资本对农业总产值的长期影响(即长期乘数)为1.2550,即从长期看,人均人力资本投入增加一个单位将使得农业总产值增加1.2550个单位;贵州省农村金融发展对农业经济增长的影响作用滞后两年左右,且农村金融发展对农业总产值的长期影响(即长期乘数)为1.3785,即从长期看,农村存贷款余额增加一个单位将使得农业总产值增加1.3785个单位;物流发展对农业经济增长的影响会滞后三年左右,且物流发展对农业总产值的长期影响(即长期乘数)为0.00171,即从长期看,货物周转率增加一个单位将使得农业总产值增加0.00171个单位;农村信息化发展对农业经济增长的影响作用滞后三年左右,且农村信息化对农业总产值的长期影响(即长期乘数)为0.8821,即从长期看,农村信息化指数增加一个单位将使得农业总产值增加0.8821个单位。
3.3贵州省农业生产效率实证分析
(一)生产效率测算方法
选择柯布——道格拉斯生产函数的随机前沿模型,以贵州省各州(市、地)乡村农业从业人员数、农业常用耕地面积、化肥施用量、农业机械总动力和农林水事务财政支出作为自变量,以第一产业总值作为因变量。测算贵州省农业生产效率的方法、步骤如下:(1)应用普通最小二乘法得出模型的参数估计;(2)由(1)估计的参数计算模型因变量的估计值;(3)计算实际值与估计值的残差;(4)取残差的最大值加上模型常数项的估计值得出常数项估计值的修正值,作为随机前沿模型的常数项。
(二)数据说明
选取贵州省2004-2008年各州(市、地)第一产业总值为因变量,乡村农业从业人员数、农业常用耕地面积、化肥施用量、农业机械总动力、农林水事务财政支出为因变量。而且,第一产业总值与农林水事务财政支出均采用以2004年为基期居民消费价格指数的进行了价格平减。数据均来源于《贵州统计年鉴》(2005~2009年,历年)。
(三)模型及估计结果
由于农业产值除了受价格因素影响之外,还可能受到气候的影响。因此,在模型中增加一个时间变量以控制气候因素。以时间除以基于同一个基期(2003年)的各州(市、地)居民消费价格指数作为气候控制变量。模型依然采用柯布——道格拉斯生产函数的形式,将模型设定为:
 (1) (1)
(1)式中, 、 、 、 、 、 、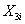 、 、 、 、 、 、 分别表示第 分别表示第 年各州(市、地)农业产值、乡村农业从业人员数、农业耕地面积、化肥施用量、农业机械总动力、农林水事务财政支出和气候指标。 年各州(市、地)农业产值、乡村农业从业人员数、农业耕地面积、化肥施用量、农业机械总动力、农林水事务财政支出和气候指标。
通过Eviews6.0,得到初步估计结果如表5所示。
表5生产技术效率函数模型估计结果
|
变量
|
系数
|
标准差
|
t值
|
p值
|
|
LNX1
|
-0.854604
|
0.130699
|
-6.538737
|
0.0000
|
|
LNX2
|
1.853179
|
0.165566
|
11.19300
|
0.0000
|
|
LNX3
|
-0.318214
|
0.049761
|
-6.394829
|
0.0000
|
|
LNX4
|
-0.329712
|
0.064128
|
-5.141470
|
0.0000
|
|
LNX5
|
0.410594
|
0.031884
|
12.87769
|
0.0000
|
|
LNW
|
1.105372
|
0.231905
|
4.766492
|
0.0000
|
|
C
|
5.190282
|
1.021067
|
5.083197
|
0.0000
|
|
R
|
0.9990
|
F统计量
|
6423.2290
|
|
调整后的R
|
0.9989
|
F统计量的p值
|
0.0000
|
|
残差平方和
|
0.0019
|
D-W 统计量
|
1.9348
|
| |
|
|
|
|
|
从上表可以看出,模型的整体效果较好,估计结果均在1%水平上显著。D-W统计量的值为1.93,查表可得,在5%的显著性水平上,d=1.24,d=1.84,所以du<1.93<4-du,模型不存在显著的自相关问题。且在模型的估计过程中采用了加权最小二乘法消除了异方差。因此,可以认为,该计量经济模型符合最小二乘法的古典假设,结果是可靠的。
(四)油菜籽生产效率的测算
将表5中的系数估计值带入(1)式,运用投入产出数据及气候指标得到农业产值的估计值,进而得到农业产值的实际值与估计值的残差,取残差的最大值加上表5中的常数项估计值作为常数项估计值的修正值,再将此修正值带入(1)式,运用投入产出数据及气候指标便可计算得到2004~2008年贵州省农业生产前沿产值,然后将实际产值除以前沿产值,便得到2004~2008年贵州省农业生产效率,计算结果见表5-21。
表6贵州省农业生产效率测算结果(2004~2008年)
|
州(市、地)
|
2004年
|
2005年
|
2006年
|
2007年
|
2008年
|
平均
|
|
贵阳市
|
0.7856
|
0.9750
|
0.7872
|
0.8945
|
0.8702
|
0.8625
|
|
六盘水市
|
0.5908
|
0.6969
|
0.6227
|
0.5962
|
0.5278
|
0.6069
|
|
遵义市
|
0.7763
|
1.0000
|
0.7532
|
0.6568
|
0.6642
|
0.7701
|
|
安顺市
|
0.7147
|
0.9190
|
0.8232
|
0.7910
|
0.8969
|
0.8290
|
|
铜仁地区
|
0.7194
|
0.9196
|
0.9245
|
0.8785
|
0.9219
|
0.8728
|
|
黔西南州
|
0.5938
|
0.8373
|
0.7326
|
0.7164
|
0.7069
|
0.7174
|
|
毕节地区
|
0.7033
|
0.8965
|
0.7870
|
0.8146
|
0.7388
|
0.7880
|
|
黔东南州
|
0.7068
|
0.9462
|
0.7856
|
0.8584
|
0.7612
|
0.8116
|
|
黔南州
|
0.7459
|
0.9721
|
0.9129
|
0.9468
|
0.9505
|
0.9056
|
|
平均
|
0.7041
|
0.9070
|
0.7921
|
0.7948
|
0.7820
|
0.7960
|
(五)测算结果分析
由表5可知,劳动力对农业总产值的弹性系数为负数,说明贵州省存在过多的农村劳动力。农业耕地面积的弹性系数为1.85,表明农业耕地面积每增加1%,则农业总产值将增长1.85%,因而贵州省农业经济的增长主要是粗放式的增长。财政支农支出的弹性系数为0.41,表明财政支农支出每增加1%,则农业总产值将增长0.41%,因而财政支农支出对农业经济增长有重要的促进作用。 3/4 首页 上一页 1 2 3 4 下一页 尾页 |


