| A、贵州省技术进步速度的测度
首先要从生产函数模型球的要素的产出弹性,然后计算产出和各种要素的平均增长速度,最后利用增长方程计算技术进步速度。增长速度方程方法中,把x1,x4,x5,x8,x9,x10的投入以外的所有因素全部归于技术进步之中。

 :技术进步速度; :技术进步速度;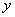 、 、 、 、 、 、 、 、 、 、 、 、 均为平均增长率。 均为平均增长率。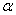 、 、 、 、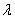 、 、 、 、 、 、 均为各要素投入弹性系数。 均为各要素投入弹性系数。
可求得 =0.0154。 =0.0154。
B、技术进步对贵州省农业经济增长贡献的测度
技术进步对农业经济增长的贡献为:
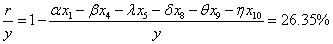
贵州省1978~2008年农业经济增长的科技进步贡献率为26.35%。这表明,农业经济增长的26.5%可以用科技进步来解释。由上表可知,各要素投入弹性系数之和小于1,这说明,当各变量同时增加1%时,农业总产值将增加小于1%,说明在技术条件不变的前提下,农业经济增长表现为规模效益递减的趋势。
(3)农业产业结构变化对农业总产值的影响
分析农业产业结构变动对农业经济增长的影响,采用以农林牧渔总产值为因变量,以资本投入(ZBTR)为主要控制自变量(由(1)分析可知),NY、LY、MY、YY分别为农业、林业、牧业、渔业占总产值比重。有下表3可知,农业结构变动对农业经济增长具有显著的影响作用。其中,林业的结构变动对农业经济增长的作用最显著,其次是牧业、农业、渔业。
表3农业产业结构变动模型估计结果
|
变量
|
系数
|
标准差
|
t值
|
p值
|
|
ZBTR
|
2.643308
|
0.057876
|
45.67159
|
0.0000
|
|
NY
|
1.410293
|
0.217876
|
6.472911
|
0.0000
|
|
LY
|
8.480332
|
0.346278
|
24.48993
|
0.0000
|
|
MY
|
2.011138
|
0.213111
|
9.437053
|
0.0000
|
|
YY
|
1.027695
|
0.215635
|
4.765909
|
0.0001
|
|
C
|
-172.4585
|
21.87129
|
-7.885155
|
0.0000
|
|
R
|
0.9999
|
F统计量
|
212761.9
|
|
调整后的R
|
0.9999
|
F统计量的p值
|
0.0000
|
|
残差平方和
|
2.9916
|
D-W 统计量
|
1.7256
|
| |
|
|
|
|
|
3.2贵州省农业经济增长影响因素的动态计量分析
对农业经济增长的分析,除了静态分析以外,有必要对农业经济增长进行动态分析。因为有些因素对农业经济增长的影响不是当期就能产生作用的,必须经济若干年才能起到显著作用,也即农业经济增长的影响因素存在滞后性。
对农业经济增长的影响有一定时间滞后的变量主要有制度变迁、人力资本投资、农村金融发展、物流发展水平及农村信息化。因为这些因素对农业经济增长的影响会有一定的时间滞后,因此在建立模型的过程中应该包含滞后的解释变量,即建立分布滞后模型。由于几何(考伊克)分布滞后模型假定滞后变量的诸系数按几何级数递减,从而存在一定的应用限制性,一个更加一般的模型是阿尔蒙提出的多项式分布滞后模型(PolynomialDistributionLagModel,PDL)。
多项式分布滞后模型需要确定两个因素:滞后项数k,多项式次数m。其中,滞后项数可以根据AIC准则和SC准则来确定,即选择使得AIC和SC最小的滞后项数k。而多项式次数一般可以选择二次或者三次。
(1)制度变迁的PDL模型分析

图1序列y与序列x10的交叉相关系数图
上图1所示的是序列y与序列x10最大滞后长度为16的交叉相关系数图。图的左边两列显示了序列y与序列x10的滞后(lag)交叉相关系数图和先行(lead)交叉相关系数图。由于本文需要考察的是序列y与序列x10的滞后交叉相关,因此只需要观察左边的交叉相关图。
图1的左边第一列显示出序列y与序列x10的滞后交叉相关系数基本上呈指数衰减,滞后长度越大,两者的相关系数越小。图的右边,lag列给出了序列y与序列x10各阶滞后的交叉相关系数,可以看到:序列y与序列x10的0阶、1阶、2阶、3阶、4阶、5阶滞后的相关系数分别为0.8854、0.8136、0.7378、0.6624、0.5811、0.5180;大于6阶的滞后,这两个序列的交叉相关系数小于0.5。因此,根据序列y与序列x10滞后交叉相关系数的分析,分布滞后模型的最大滞后长度应该小于6。为了比较分析,建立滞后长度k分别为2、3、4、5的分布滞后模型。表4为无约束限制的分布滞后模型估计结果。从所估计模型的 、AIC准则及SC准则这些值可以判断,模型滞后长度为2且多项式次数为2的模型优于其他模型。 、AIC准则及SC准则这些值可以判断,模型滞后长度为2且多项式次数为2的模型优于其他模型。
表4多个无约束限制的制度变迁分布滞后模型估计结果
|
模型滞后长度
|
多项式次数
|

|
AIC准则
|
SC准则
|
|
2
|
2
|
0.7368
|
8.3523
|
8.5409
|
|
3
|
2
|
0.7208
|
8.3414
|
8.5317
|
|
3
|
3
|
0.7089
|
8.4118
|
8.6497
|
|
4
|
2
|
0.6922
|
8.3677
|
8.5596
|
|
4
|
3
|
0.6792
|
8.4387
|
8.6786
|
|
5
|
2
|
0.6684
|
8.3894
|
8.5829
|
|
5
|
3
|
0.6527
|
8.4663
|
8.7082
|
对滞后长度为2且多项式次数为2的模型进行修正,最后得到的结果如下图2所示:
 
图2制度变迁的PDL模型估计结果
图2所示的输出结果的上半部分中的PDL01、PDL02分别代表式(5.3.4)中的 、 、 。由于多项式次数为2,且加入近端约束,因此除了常数项外共有2个系数估计值。PDL01与PDL02的系数估计值在5%的检验水平是显著的,而且F统计量=968.1408,其相应的概率值P为0,从而可以拒绝“整体上诸PDL变量对y没有影响”的原假设,再则 。由于多项式次数为2,且加入近端约束,因此除了常数项外共有2个系数估计值。PDL01与PDL02的系数估计值在5%的检验水平是显著的,而且F统计量=968.1408,其相应的概率值P为0,从而可以拒绝“整体上诸PDL变量对y没有影响”的原假设,再则 =0.9857,非常接近1,说明模型总体模拟效果非常好。 =0.9857,非常接近1,说明模型总体模拟效果非常好。
图2的下半部分,LagDistributionofx10列绘出了分布滞后变量x10的诸 系数的分布图,其图形大致是二次抛物线形状。 系数的分布图,其图形大致是二次抛物线形状。 2/4 首页 上一页 1 2 3 4 下一页 尾页 |


