| (二)估计方法
门槛分析关键是要解决两方面的问题:一是联合估计门槛值 和 和 ;二是进行门槛效应的相关检验。为了对模型(3)进行参数估计:1.要消除个体效应 ;二是进行门槛效应的相关检验。为了对模型(3)进行参数估计:1.要消除个体效应 的影响,常用方法是从每个观察值中减去组内平均值,再将所有观察值进行类叠;2.门槛值 的影响,常用方法是从每个观察值中减去组内平均值,再将所有观察值进行类叠;2.门槛值 可能是变量 可能是变量 取值范围内的任意值,若从中任意选取一个值 取值范围内的任意值,若从中任意选取一个值 作为初始值赋予 作为初始值赋予 后,便可采用OLS法估计斜率 后,便可采用OLS法估计斜率 , 斜率 , 斜率 估计出来后,便可计算出对应的残差平方和 估计出来后,便可计算出对应的残差平方和 ;3.同样,再在 ;3.同样,再在 取值范围内选择另一个值 取值范围内选择另一个值 ,计算出相应的斜率和残差平方和 ,计算出相应的斜率和残差平方和 ;4.将两次残差平方和进行比较,较小的 ;4.将两次残差平方和进行比较,较小的 对应的 对应的 值作为此时的初始值付给 值作为此时的初始值付给 ;5.如此往复至从变量 ;5.如此往复至从变量 取值范围内搜索到一个值,使得OLS法估计模型得到的残差平方和最小,此时值则为要估计的门槛值 取值范围内搜索到一个值,使得OLS法估计模型得到的残差平方和最小,此时值则为要估计的门槛值 ,进而估计出 ,进而估计出 。实际中,逐步搜索法的计算速度很慢,我们可以采用格栅搜索法进行搜索。 。实际中,逐步搜索法的计算速度很慢,我们可以采用格栅搜索法进行搜索。
门槛模型参数估计完后,需要进行门槛分析的相关检验,主要包括两方面检验:一是门槛值的显著性检验;二是门槛值的真实性检验。前者原假设为: ,检验统计量为: ,检验统计量为: (4) (4)
其中, 为在原假设下进行参数估计后得到的残差平方和, 为在原假设下进行参数估计后得到的残差平方和, 为备则假设下进行参数估计后得到的残差方差。在原假设下门槛值 为备则假设下进行参数估计后得到的残差方差。在原假设下门槛值 是不确定的,因此统计量 是不确定的,因此统计量 的分布为非标准分布,但可采用“自抽样”模拟其渐进分布,进而构建其对应的P值。第二个检验的原假设为 的分布为非标准分布,但可采用“自抽样”模拟其渐进分布,进而构建其对应的P值。第二个检验的原假设为 ,相应的似然比检验统计量为: ,相应的似然比检验统计量为:
 (5) (5)
统计量 的分布也是非标准的,但Hansen提供了一个简单的公式计算出其拒绝域,即当 的分布也是非标准的,但Hansen提供了一个简单的公式计算出其拒绝域,即当 时,拒绝原假设,其中 时,拒绝原假设,其中 为显著性水平。同样,以上参数估计及假设检验是针对单门槛的情况,双门槛模型的相关性检验与之相似,此处不再详细叙述。 为显著性水平。同样,以上参数估计及假设检验是针对单门槛的情况,双门槛模型的相关性检验与之相似,此处不再详细叙述。
(三)数据说明
本文采用1998-2007年我国29个省份的数据进行实证研究。其中需要说明的是 指标。国摘要的理论和现实意义。证的结果大多为负,造成的假象好像是我国金融发展根本没有促进经济增长中国论文网。所以该指标并不能真实的衡量我国金融发展水平,而是相当程度上高估了其水平金融论文,张军等(2005)认为以非国有企业的贷款规模与GDP之比来衡量中国的金融发展水平较为合适,林毅夫(2006)认为中国是银行主导的金融发展模式,而以中小银行的市场份额来衡量银行业机构的优化更为有效,周立(2002)构造了金融市场化比率来衡量金融发展的程度。本文也选取非国有部门贷款与GDP之比来衡量,且假设全部信贷只分配给国有企业和非国有企业两部分,进一步假设各省分配到国有企业的贷款与该省国有企业的固定资产投资成正比,则非国有部门贷款为:总贷款余额 指标。国摘要的理论和现实意义。证的结果大多为负,造成的假象好像是我国金融发展根本没有促进经济增长中国论文网。所以该指标并不能真实的衡量我国金融发展水平,而是相当程度上高估了其水平金融论文,张军等(2005)认为以非国有企业的贷款规模与GDP之比来衡量中国的金融发展水平较为合适,林毅夫(2006)认为中国是银行主导的金融发展模式,而以中小银行的市场份额来衡量银行业机构的优化更为有效,周立(2002)构造了金融市场化比率来衡量金融发展的程度。本文也选取非国有部门贷款与GDP之比来衡量,且假设全部信贷只分配给国有企业和非国有企业两部分,进一步假设各省分配到国有企业的贷款与该省国有企业的固定资产投资成正比,则非国有部门贷款为:总贷款余额 (1-国有经济固定资产投资总额/全社会固定资产投资总额);此外, (1-国有经济固定资产投资总额/全社会固定资产投资总额);此外,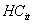 指标,采用6岁以上人口平均受教育年数来衡量,即设文盲半文盲、小学、初中、高中、大专以上教育程度的居民平均年数分别为0、6、9、12和16年,然后再计算加权平均值即可; 指标,采用6岁以上人口平均受教育年数来衡量,即设文盲半文盲、小学、初中、高中、大专以上教育程度的居民平均年数分别为0、6、9、12和16年,然后再计算加权平均值即可; 用各地区外商直接投资实际利用额与名义GDP之比表示; 用各地区外商直接投资实际利用额与名义GDP之比表示; 、 、 、 、 的含义如前所述,其中 的含义如前所述,其中 历年数据都以1998年为不变价格进行了折算。相关描述性统计见表1。 历年数据都以1998年为不变价格进行了折算。相关描述性统计见表1。
表1样本描述性统计量(1998―2007,N=29地区,T=10年,NT=290)
|
变量
|
变量含义及数据来源
|
平均值
|
标准差
|
最小值
|
最大值
|
|
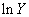
|
专利申请量(项),数据来源:《中国科技统计年鉴》
|
7.769
|
1.157
|
4.564
|
10.941
|
|

|
科技活动人员数,同上
|
2.151
|
0.951
|
-1.021
|
3.804
|
|

|
科技活动经费内部支出总额,同上
|
4.123
|
1.245
|
0.571
|
6.696
|
|

|
外商直接投资额与名义GDP之比,数据来源《中国统计年鉴》
|
0.026
|
0.026
|
0.001
|
0.134
|
|
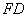
|
金融发展,选取非国有部门贷款与GDP之比来衡量,数据来源:《金融统计年鉴》
|
0.553
|
0.219
|
0.029
|
1.499
|
|

|
产业结构,用第二产业占GDP得比重表示,数据来源:《中国统计年鉴》
|
0.439
|
0.077
|
0.197
|
0.599
|
|

|
人力资本,用平均受教育年限表示,数据来源:《中国人口统计年鉴》
|
7.869
|
0.944
|
5.265
|
10.969
|
四、实证结果分析
对模型(1)进一步研究发现,科技活动人员数量和科技活动经费内部支出有较高的相关性,对数据进行相关性分析发现,从事科技活动人员数量和专利申请量的相关性较弱,故将其去掉。变量间的相关系数矩阵见表2。
表2变量的相关系数矩阵
|
|
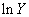
|

|

|

|
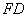
|

|

|
|
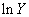
|
1
|
|
|
|
|
|
|
|

|
0.8515
|
1
|
|
|
|
|
|
|

|
0.8856
|
0.9259
|
1
|
|
|
|
|
|

|
0.3592
|
0.1624
|
0.2398
|
1
|
|
|
|
|
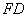
|
0.434
|
0.2275
|
0.4061
|
0.3575
|
1
|
|
|
|

|
0.514
|
0.5076
|
0.5169
|
0.0624
|
-0.1056
|
1
|
|
|

|
0.4366
|
0.3501
|
0.5232
|
0.331
|
0.5963
|
0.123
|
1
|
接下来,我们对模型(1)进行实证金融论文,对于面板数据的实证通常有混合最小二乘法、固定效应和随机效应三种模型可供选择,实证时应根据样本数据情况进行选择,本文最终选择固定效应,结果见表3。
表3固定效应模型的检验结果
|
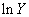
|
系数
|
标准误
|
T值
|
P值
|
95%的置信区间
|
|

|
0.318
|
0.049
|
6.50
|
0.000
|
0.22
|
0.414
|
|

|
-0.793
|
1.112
|
-0.71
|
0.476
|
-2.983
|
1.397
|
|
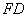
|
0.927
|
0.146
|
6.35
|
0.000
|
0.639
|
1.214
|
|

|
2.255
|
0.632
|
3.57
|
0.000
|
1.012
|
3.499
|
|

|
0.095
|
0.051
|
1.86
|
0.065
|
0.006
|
0.196
|
检验结果表明,FDI对我国的自主创新整体上并不显著,而且表现出一定程度上的负向影响,远没有成为推动我国自主创新的动力;而科研经费、金融发展水平、产业结构升级与人力资本水平与我国的自主创新均呈正相关关系。
下面我们试着来验证本文的假说即检验金融发展、FDI与我国自主创新是存在门槛效应的。首先进行门槛效应检验,表4报告了三种假设下进行门槛效应检验后的F值和P值。不难发现:单门槛效应在5%的显著性水平下显著,双门槛效应在1%的显著性水平下显著,而三门槛效应却不显著,其自抽样P值为0.51,故后本文选用双门槛模型进行分析。
表4 门槛效应检验
|
模型
|
F值
|
P值
|
BS次数
|
1%
|
5%
|
10%
|
|
单一门槛
|
15.941
|
0.050
|
300
|
32.001
|
16.109
|
10.483
|
|
双重门槛
|
17.042
|
0.000
|
300
|
13.865
|
8.252
|
6.655
|
|
三重门槛
|
1.578
|
0.510
|
300
|
17.066
|
7.780
|
6.045
|
门槛效应检验过后,需要就双门槛模型的两个门槛值进行估计和检验,表5报告了双门槛模型门槛值的估计结果以及门槛值的95%置信区间。图1、2、3分别为单一门槛模型、双门槛模型参数与似然值的关系图,图中虚线为似然比统计量临界值,在5%的显著性水平下,似然比统计量的临界值为7.35。从图1和图2不难看出:当门槛1估计值为0.642和门槛2估计值为0.954时,似然比值接近于0;当门槛值1处于[ 0.631,0.688 ]区间内和门槛2处于[ 0.954,0.986 ]区间内时,似然比值小于5%显著性水平下的临界值,处于原假设接受域内,即两个门槛值都与实际门槛值相等。门槛 和门槛 和门槛 估计出来后便可对双门槛模型进行参数估计,其参数估计结果列于表6。 估计出来后便可对双门槛模型进行参数估计,其参数估计结果列于表6。
2/3 首页 上一页 1 2 3 下一页 尾页 |


