论文摘要:新教材有待改进的几个地方-论文网
论文关键词:新教材,有待,改进,几个,地方
随着课改的不断深入,在有关专家和广大一线教师的努力下,现编普通高中课程标准实验教科书《数学》,已经过多次修改,应该说,无论是内容还是结构上,都日趋完善.但笔者经过认真分析,发现依然存在一些有待改进的地方:
一、条件描述错误;
题目1把函数 在 在 和 和 之间的一段图象近似地看作直线,且设 之间的一段图象近似地看作直线,且设 ,试用 ,试用 , , 来估计 来估计 。 。
(见普通高中课程标准实验教科书《数学》必修(2)P116页28题)
分析:因为直线两端是无限延伸的,两点之间的部分只能是线段。虽然题目所表达的意思大家都能理解,但数学语言毕竟不同于生活语言,它的表述必须是严密无误的,建议将“直线”改成“线段”
二、解答过程错误
题目2:写出命题”平行四边形的对边相等”的否定.
(见苏教版普通高中标准实验教科书《数学》1-1P15页例1(3))
书中给出的解答是:“平行四边形的对边相等”表示任意一个平行四边形的对边相等,它的否定是“存在平行四边形,它的对边不相等”
分析:易知,四边形的对边有两组,命题”平行四边形的对边相等”的本意可以这样描述:“任意一个平行四边形的两组对边分别相等”。这里的结论有两方面:即“两组对边分别相等”,且同时成立。因此,它的否定应包括两种情形:“恰有一组对边相等,而另一组对边不相等”和“两组对边均不相等”,显然,书中的解答丢掉了第一种情形,因此是不严密的。
正确的解答可以这样描述:
“平行四边形的对边相等”表示任意平行四边形的两组对边分别相等,它的否定是“存在平行四边形,它的对边不都相等”。
或“平行四边形的对边相等”表示任意平行四边形的两组对边分别相等,它的否定是“存在平行四边形,至少有一组对边不相等”。
题目3设计一个正四棱锥冷水塔,高是 ,底面的边长是 ,底面的边长是 ,制造这种塔顶需要多少平方米铁板?(保留两位有效数字) ,制造这种塔顶需要多少平方米铁板?(保留两位有效数字)
(见普通高中课程标准实验教科书《数学》必修(2)P48页例1)
书中给出的解答过程有这样一段:
设 是斜高。在 是斜高。在 中,根据勾股定理。得 中,根据勾股定理。得 ,所以 ,所以 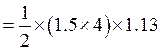  。 。
分析:,由于斜高 是一个近似值,在正棱锥的侧面积公式代入数据时,应用约等号“ 是一个近似值,在正棱锥的侧面积公式代入数据时,应用约等号“ ”,应改成: ”,应改成:   。 。
三、与实际不吻合;
题目4一铁棒欲通过如图所示的直角走廊,试回答下列问题:
 ⑴证明棒长 ⑴证明棒长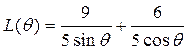 ; ;
⑵当 时,作出上述函数的图象; 时,作出上述函数的图象;
(可用计算器或计算机)
⑶由⑵中的图象求 的最小值; 的最小值;
(用计算器或计算机)
⑷解释⑶中所求得的 是能通过这个直角走廊的铁棒的长度的最大值。 是能通过这个直角走廊的铁棒的长度的最大值。
(见普通高中课程标准实验教科书《数学》必修(4)P49页第17题)
关于第(4)小题,教学参考书提供的解答是这样的:
若铁棒长不大于 ,则铁棒能在这个直角走廊拐弯;若铁棒长大于 ,则铁棒能在这个直角走廊拐弯;若铁棒长大于 ,则铁棒不能在这个直角走廊拐弯,故 ,则铁棒不能在这个直角走廊拐弯,故 是能通过这个直角走廊的铁棒中的最长者。 是能通过这个直角走廊的铁棒中的最长者。
笔者认为,这一小题的设计与解答是值得商榷的,分析如下:
易知,这是一个直角走廊的俯视图,如果要使铁棒“水平”移动通过它,结论(4)显然是合理的。但我们知道,直角走廊应是一个立体空间图形,在铁棒长取最大值 时的位置的垂直平面内,铁棒若“倾斜”放置,则更长一些的时候,有时也可通过。如果直角走廊的高度是 时的位置的垂直平面内,铁棒若“倾斜”放置,则更长一些的时候,有时也可通过。如果直角走廊的高度是 ,则实际能通过这个直角走廊的铁棒的长度的最大值 ,则实际能通过这个直角走廊的铁棒的长度的最大值  。 。
因此,第(4)小题的设计与解答和现实生活是不协调的,其设计建议作如下修改:
方案一:删除第(4)小题;
方案二:改为“要使铁棒水平移动通过,解释⑶中所求得的 是能通过这个直角走廊的铁棒的长度的最大值”; 是能通过这个直角走廊的铁棒的长度的最大值”;
方案三:改为“若直角走廊的高度是 ,求能通过这个直角走廊的铁棒的长度的最大值”. ,求能通过这个直角走廊的铁棒的长度的最大值”.
应该肯定,新课程出现了一些鲜活、生动、切合实际的题型设计、解题思路。给数学教学注入了新的血液,深得一线教师的广泛认可。我们有理由相信,只要大家集思广益,课改 |


