|
Gls
|
GWs
|
GWs+rm-rs
|
rm
|
rm-rs
|
rm+rs
|
rs
|
|
平均值
|
3.44
|
0.87
|
1.91
|
5.9
|
1.04
|
10.75
|
4.85
|
|
中值
|
2.71
|
0.14
|
1.87
|
6.56
|
1.73
|
11.39
|
4.83
|
|
最大值
|
12.87
|
11.74
|
18.19
|
17.95
|
17.52
|
30.65
|
22.87
|
|
最小值
|
-1.11
|
-9.97
|
-17.35
|
-13.86
|
-17.22
|
-28.35
|
-14.49
|
|
标准差
|
2.85
|
5.25
|
7.62
|
6.47
|
7.15
|
12.49
|
7.86
|
|
样本量
|
30
|
30
|
30
|
30
|
30
|
30
|
30
|
数据来源：依据历年《中国统计年鉴》相关原始数据整理计算。
（二）回归分析
1．整体时间序列数据回归。由于时间序列数据样本量不大，因此首先对变量Gls、rm、rs和GWs进行Jarque-Bera检验，基本符合正态分布规律，从而其组合形成的回归量也符合OLS对回归变量正态分布的要求，它们的Kernel 密度分布如图5表示。利用上述数据对改进后的非均衡增长模型进行回归分析，结果如表2所示，其中，回归模型Gls1和Gls2是利用上述数据对程大中（2004）模型的重新验证。比较可以发现，加入行业间工资差异变动规律之后的模型解释力有超过十个百分点的提高；并且单纯的OLS回归即模型Gls3的结存在自相关性，因此，添加应变量一阶滞后项，如模型Gls4所示，此时结果较优，表明前一年第三产业就业增长率具有正向的延续影响，由回归模型Gls4的结果可得：
Gls=1.85-0.25 (GWs+rm-rs)+0.38(rm+rs)-0.75 rs+0.43Gls(-1)
(2.45**) (-3.12***) (3.82***) (-3.62***)(2.45***)
   
图5 变量的Kernel密度分布图6 时间序列回归的拟合与预测
检验该模型的异方差性。用White检验方法将残差平方与解释变量的一次项、二次项和交叉项进行回归，得 ，通过 分布比较可知 ，接受原假设，随机误差项不存在异方差性。该模型的F检验量为6.22，在1％水平上显著，整体能通过检验；各解释变量的t检验显著性均在10％以上；此时Durbin-Watson检验值为2.04，不存在自相关性；R2为0.51，其解释能力较好；用Wald统计量检验 、 和 ，发现在5％的置信度上无法拒绝备责假设，表明原先的模型能够得到经验数据的支持。利用上述模型对1980至2008年的第三产业就业比重增长率进行拟合，如图6表示论文怎么写。除1994年差距较大以外，波动趋势比较一致，特别是近十年来拟合效果的残差较小。
表2不同时间序列模型的回归结果
|
模型 变量
|
常数项
|
rm
|
rm-rs
|
rs
|
rm+rs
|
GWs+rm-rs
|
Gls滞后项
|
F
|
R2
|
AR2
|
DW
|
|
Gls1
|
3.00***
|
0.06
|
0.10*
|
|
|
|
|
1.43
|
0.10
|
0.03
|
1.13
|
|
(4.26)
|
(0.66)
|
(1.24)
|
|
|
|
|
|
Gls2
|
1.46*
|
0.04
|
0.13*
|
|
|
|
0.47**
|
3.74
**
|
0.31
|
0.23
|
1.75
|
|
(1.69)
|
(0.52)
|
(1.79)
|
|
|
|
(2.77)
|
|
Gls3
|
3.26***
|
|
|
-0.70*
|
0.37***
|
-0.27***
|
|
4.19
**
|
0.33
|
0.25
|
1.31
|
|
(5.22)
|
|
|
(-2.80)
|
(3.56)
|
(-2.97)
|
|
|
Gls4
|
1.85**
|
|
|
-0.75***
|
0.38***
|
-0.25***
|
0.43***
|
6.22
***
|
0.51
|
0.43
|
2.04
|
|
(2.45)
|
|
|
(-3.62)
|
(3.82)
|
(-3.12)
|
(2.45)
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
注：*、**和***分别表示估计值在1％，5％和10％的置信度水平上显著，下方括号内为系数的t检验值。
表31993－2008年各省的截面和面板数据回归结果
|
模型 变量
|
常数项
|
rs
|
rm+rs
|
GWs+rm-rs
|
F
|
R2
|
AR2
|
回归方法（权重）
|
|
Gls1994
|
10.35***
|
-1.34***
|
0.34**
|
-0.39***
|
19.92***
|
0.71
|
0.67
|
截面OLS
|
|
(6.00)
|
(-4.40)
|
(1.97)
|
(-3.08)
|
|
Gls1995
|
2.85***
|
-0.63***
|
0.31***
|
-0.21**
|
7.28***
|
0.47
|
0.40
|
截面OLS
|
|
(4.19)
|
(-4.51)
|
(4.15)
|
(-2.19)
|
|
Gls1996
|
4.13***
|
-0.49**
|
0.19*
|
-0.149
|
4.84***
|
0.37
|
0.29
|
截面OLS
|
|
(6.23)
|
(-2.53)
|
(1.57)
|
(-1.44)
|
|
Gls1997
|
-1.24
|
-0.73***
|
0.58***
|
-0.31***
|
15.94***
|
0.75
|
0.72
|
截面WLS（rs2）
|
|
(-0.75)
|
(-5.13)
|
(6.71)
|
(-4.57)
|
|
Gls1998
|
5.68***
|
-0.75***
|
0.32***
|
-0.35***
|
28.59***
|
0.88
|
0.87
|
截面WLS（rs2）
|
|
(3.86)
|
(-6.78)
|
(8.11)
|
(-4.59)
|
|
Gls1999
|
8.75***
|
-0.91***
|
0.14
|
-0.24***
|
69.76***
|
0.79
|
0.76
|
截面WLS（1/ rm）
|
|
(11.27)
|
(-7.96)
|
(1.49)
|
(-3.98)
|
|
Gls2000
|
8.41***
|
-1.23***
|
0.35***
|
-0.36***
|
51.28***
|
0.86
|
0.84
|
截面OLS
|
|
(8.68)
|
(-9.32)
|
(3.86)
|
(-4.06)
|
|
Gls2001
|
2.14
|
-0.73***
|
0.35**
|
-0.08
|
14.49***
|
0.78
|
0.75
|
截面WLS（rm2）
|
|
(1.51)
|
(-3.44)
|
(2.47)
|
(-1.03)
|
|
Gls2002
|
5.38***
|
-0.73***
|
0.23**
|
-0.31**
|
20.52***
|
0.71
|
0.68
|
截面OLS
|
|
(6.72)
|
(-4.75)
|
(2.26)
|
(-2.64)
|
|
Gls2003
|
1.08
|
-0.93***
|
0.36***
|
-0.18**
|
57.60***
|
0.91
|
0.90
|
截面WLS（rm2）
|
|
(0.73)
|
(-11.08)
|
(5.44)
|
(-2.47)
|
|
Gls2004
|
6.32***
|
-0.83***
|
0.13**
|
-0.01
|
21.25***
|
0.66
|
0.62
|
截面WLS（rs2）
|
|
(7.00)
|
(-4.57)
|
(2.20)
|
(-0.11)
|
|
Gls2005
|
0.74
|
-0.56***
|
0.29***
|
-0.27***
|
8.31***
|
0.62
|
0.58
|
截面WLS（rm2）
|
|
(0.73)
|
(-3.37)
|
(3.53)
|
(-3.53)
|
|
Gls2006
|
0.70
|
-0.73*
|
0.12***
|
0.01
|
10.33***
|
0.96
|
0.95
|
截面WLS（rm2）
|
|
(0.80)
|
(-1.77)
|
(2.95)
|
(0.11)
|
|
Gls2007
|
2.91***
|
-0.76***
|
0.06***
|
-0.12***
|
22.52***
|
0.73
|
0.70
|
截面OLS
|
|
(5.75)
|
(-5.02)
|
(3.05)
|
(-4.80)
|
|
Gls2008
|
3.76***
|
-0.73***
|
0.18**
|
-0.10*
|
16.61***
|
0.67
|
0.63
|
截面OLS
|
|
(4.65)
|
(-5.51)
|
(2.17)
|
(-1.47)
|
|
Glspool
|
—
|
-0.39***
|
0.20***
|
-0.06***
|
1.3
|
0.12
|
0.1
|
混合面板
|
|
—
|
(-9.04)
|
(0.91)
|
(-2.90)
|
|
Glsrandom
|
4.64***
|
-0.29***
|
0.09***
|
-0.10***
|
38.26***
|
0.21
|
0.20
|
随机效应面板
|
|
(6.18)
|
(-8.50)
|
(4.21)
|
(-4.69)
|
|
Glsfix
|
3.27***
|
-0.38***
|
0.11***
|
-0.10***
|
8.07***
|
0.30
|
0.25
|
固定效应面板
|
|
(10.75)
|
(-8.72)
|
(5.16)
|
(-4.93)
|
注：*、**和***分别表示估计值在1％，5％和10％的置信度水平上显著，下方括号内为系数的t检验值。截面数据模型采用的回归方法包括最小二乘法（OLS）和加权最小二乘回归（WLS），面板数据模型采用的回归模型包括混合面板数据模型、随机效应模型和固定效应模型。所有模型的方法和权重如最后一列所示，面板数据模型的时间固定回归结构此处省略报告。
2．省际截面数据和面板数据回归。采用1994－2008各省的截面数据，可得各年的回归结果如表3中模型Gls1994—Gls2008所示。对所有普通最小二乘回归结果进行White检验第三产业，发现部分模型存在异方差性，因此采用加权最小二乘回归（WLS）方法对模型进行了调整。用Wald统计量验证备责假设、和，结果在5％的置信度下，只有模型Gls1995和Gls1996拒绝了原假设；同时，从各个模型的调整后可决系数比较发现，90年代中期之前截面样本回归模型的AR2总体上相对低些。这两项特征说明理论模型的适用性和解释能力在近期提高，这表明随着产业结构转型的深化，影响中国第三产业就业吸纳能力的因素与理论分析所描述的状况逐步吻合。同时，对各省1994-2008面板数据进行分析，混合面板数据模型、随机效应模型和固定效应模型的结果分别如表3模型Glspool、Glsrandom和Glsfix所示，结果发现混合面板数据模型的方程整体解释效果不佳（F检验值在10%水平上不显著），采用Hausman 检验对随机效应模型和固定效应模型进行筛选，结果发现后者较优秀，因而采用固定效应模型的结果。
从不同省市截面数据的回归分析可知，影响三产就业吸纳能力在不同区域间呈现较大差异的主要原因与理论模型命题相符；而对全国时间序列数据的分析也表明影响同一区域不同发展阶段的就业吸纳能力的主要因素包括了劳动生产率、产业间工资差异等。处于不同发展水平区域的三产就业吸纳能力与同一区域不同发展阶段的就业吸纳能力的演变具有大体上的一致性，表明在研究区域第三产业就业吸纳能力的发展趋势时，可以用普遍的规律大致推测其未来的变动方向，在此基础上增加区域内其它特征变量进行的分析将会加具科学性。
（三）价格弹性β与收入弹性α
为了便于分析服务业劳动生产率增长率相对滞后程度、服务需求价格弹性以及服务需求收入弹性三者相互作用的状况对服务业就业增长的影响，将理论模型（7）重新整理成为 。第一项中 为服务业部门劳动生产率相对滞后程度，在  的情形下，它将对服务业就业增长率的提高起正向作用。第二项表示需求收入弹性对服务业就业吸纳能力的影响，工资增长 将导致对服务需求增长 ,产出以增长，此时若服务产品需求的收入弹性较高（即 ），则有 ，即服务产出增长率大于总体增长,此时服务业就业份额会上升，否则下降。第三项反映了部门间工资差异变动率对服务业就业的影响， 且 的情形表示由于存在导致部门间劳动力市场非完全竞争的其他因素，使得部门间工资差异扩大，第三产业劳动力成本提高相对较快而对服务业就业增长率起负向作用。在程大中（2004）的模型中，由于假定行业间工资完全竞争，因此第二项简化为 ，这实际上是以制造业部门的工资增长率代替了全社会的平均状况，而第三项也因为这个假设而不存在。
 图7总结了上述所有模型中通过了检验的参数估计值，价格弹性 、收入弹性 与服务业相对劳动生产率、服务业工资差异变动程度共同作用导致了服务业的劳动吸纳能力各年间的波动。
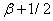 在分析的时间段，由于估计值大于-0.5，即的系数 >0成立，因而服务业部门劳动生产率相对滞后的状况对该部门就业比重增长起到了正向的作用，这意味着服务业的就业吸纳能力依赖于产品缺乏价格弹性和服务业部门低生产率的共同作用。从各年省际数据回归结果的HP滤波趋势来看，的估计值显现出不断增长的状态（图7），而服务业劳动生产率的滞后程度也不断加深（图3），两者的共同作用保证了一定时期内服务业的就业吸纳能力，但这种“低效率、低弹性”模式并不具有可持续性第三产业，一旦价格弹性随着服务业产品多样化程度而上升，或者技术进步使得劳动生产率滞后的状况有所扭转，从而单方面打破“双低水平陷阱”，而两者又无法同时达到“高效率、高弹性”的状态，那么服务业的就业保障能力将无法维持。
3/4 首页 上一页 1 2 3 4 下一页 尾页 |
