 :表示第 :表示第 年上海市 年上海市 总量的一次累加数量, 总量的一次累加数量, ; ;
 :表示第 :表示第 年上海市 年上海市 总量的预测值, 总量的预测值, ; ;
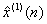 :表示第 :表示第 年上海市 年上海市 总量的一次累加数量的预测值, 总量的一次累加数量的预测值, ; ;
 :表示GM(1,1)模型中的级比检验数列, :表示GM(1,1)模型中的级比检验数列, ; ;
 :表示为 :表示为 点(或时刻)的残差, 点(或时刻)的残差, ; ;
 :表示为 :表示为 点(或时刻)的相对误差, 点(或时刻)的相对误差, ; ;
 :表示GM(1,1)模型预测结果的平均相对误差; :表示GM(1,1)模型预测结果的平均相对误差;
 :表示投入产出模型中直接经济效应的投资乘数; :表示投入产出模型中直接经济效应的投资乘数;
 :表示投入产出模型中间接经济效应的消费者边际消费倾向; :表示投入产出模型中间接经济效应的消费者边际消费倾向;
 :表示投入产出模型中,国内生产总值; :表示投入产出模型中,国内生产总值;
 :表示投入产出模型中,直接经济投资的改变量; :表示投入产出模型中,直接经济投资的改变量;
 :表示模型中全社会消费品零售总额的变化量。 :表示模型中全社会消费品零售总额的变化量。
3.1.4 GM(1,1)模型的构建
(1)微分方程的构建
运用灰色系统理论的思想,结合上海市2002~2009年 值(见表1),构建GM(1,1)模型,对在世博会影响下 值(见表1),构建GM(1,1)模型,对在世博会影响下 年上海市的 年上海市的 具体值作出合理预测。 具体值作出合理预测。
Step1.级比检验
建立上海市2002~2009年 数据的时间序列如下, 数据的时间序列如下,

求出改组时间序列的级比 向量, 向量,


作出级比判断,由于所有的
 , ,
因此可以用 作满意的GM(1,1)建模[13]。 作满意的GM(1,1)建模[13]。
Step2.对原始数据 做一次累加,即 做一次累加,即

上海市 的累加数列克服了原始数据的波动性和随机性,转化为规律性较强的递增数列,为建立微分方程形式的上海市 的累加数列克服了原始数据的波动性和随机性,转化为规律性较强的递增数列,为建立微分方程形式的上海市 预测模型做好准备。 预测模型做好准备。
Step3.构造数据数列 及数据向量 及数据向量 , ,



Step4.利用MATLAB2009a数学软件计算

Step5.建立上海市 的预测模型 的预测模型

(2)时间响应函数的求解
依据灰色系统预测理论思想,累加数列的初始值与原始时间数列的初始值应该相同,即 ,得其解(称为时间响应函数)为[14] ,得其解(称为时间响应函数)为[14]

求生成数列值 及模型的还原值 及模型的还原值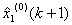 ,令 ,令 经济效益,由上面的时间响应函数可算得 经济效益,由上面的时间响应函数可算得 ,其中取 ,其中取

由 ,取 ,取 ,得 ,得


即由GM(1,1)模型预测上海市2002~2009年的 时间序列为 时间序列为 亿元。 亿元。
3.2模型的检验与求解
3.2.1 GM(1,1)模型的检验
由于文中利用基于GM(1,1)模型对上海市 的经济总量作出预测,为了判断预测和评估结果的有效性,对GM(1,1)模型进行检验,检验GM(1,1)模型的精度,我们采用残差检验的方法毕业论文格式。 的经济总量作出预测,为了判断预测和评估结果的有效性,对GM(1,1)模型进行检验,检验GM(1,1)模型的精度,我们采用残差检验的方法毕业论文格式。
定义原始时间序列 的 的 点(或时刻)的实际值为 点(或时刻)的实际值为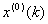 ,由 ,由 所得灰色模型的计算值为 所得灰色模型的计算值为 ,则称 ,则称 为 为 点(或时刻)的残差 点(或时刻)的残差 ;定义相对误差 ;定义相对误差 、平均相对误差 、平均相对误差 如下, 如下,
2/5 首页 上一页 1 2 3 4 5 下一页 尾页 |


