用类比思想巧解变力做功问题_求解

论文导读:：本文通过类比和挖掘完全非弹性碰撞运动在极限条件下的结论，来求解一类用常规方法较难解决的变力做功问题，使得解答这类变力做功问题变的简单。
论文关键词：变力做功，完全非弹性碰撞，求解
 

正文：在高中物理的教学中，变力做功问题是一个重点，同时也是一个难点。由于变力做功问题更贴近生活和生产的实际，因此，它有着丰富的内涵和多彩的形式，其中有这样一类问题,用通常的方法很难解答。

一、例 如；

例1．传送带以1M/S的速度水平匀速运动,一质量为20KG的物体无初速的放到传送带皮带上。若传送过程中传送带保持速率不变,求此过程中物体与皮带间的摩擦力做了多少功?( )

A 10JB 20J C30JD40J

二、解 析

在物体放到皮带上到与皮带一起匀速运动的过程中，摩擦力由动摩擦力变为静摩擦力，最后到摩擦力消失为0。整个过程中摩擦力是变力，为变力做功问题。而且，通过题意我们不能找到摩擦力的大小，和发生的位移。因此，用常规的方法求此题的摩擦力做功问题，是一个很难的任务。怎么办呢？通过审题、分析和对比，我们发现，可以将此过程与学过的完全非弹性碰撞问题结合起来，它们间有很强的相似性。

三、发 现

四、挖 掘

设在光滑的水平面上求解，有两质量分别为M₁和M₂的物体，当物体M₁以速度V₁跟静止的物体M₂正碰时粘在一起，共同速度为V，由动量守恒定理可得

免费论文。

系统损失的机械能为

解得

若M₁＞＞M₂，则V≈V₁，，而M₂获得的动能为：

这表明，当质量很大的物体与质量很小的静止物体发生完全非弹性碰撞时，前者的动能几乎不变,因此,系统损失的机械能跟后者增加的机械能几乎相等.

若保持物体恒速,则从碰撞角度而言,就相当于其质量为无穷大,由此得到结论:

在恒速物体与静止物体相互作用达到同速的过程中,被加速的物体增加多少动能,系统就增加多少内能(或势能).

由此结论我们便可以很简单的求解出例1的答案.物体在皮带上被加速所获得的动能为:

在物体加速的过程中,因为相对于皮带向后滑动而产生的热量使物体增加的内能。则过程中物体与皮带间的摩擦力做功 ，

故选项B正确.

五、应 用

例2．如图所示，在光滑的水平面上，A、B两物体的质量分别为M₁和M₂中间用一根原长为L₀、劲度系数为K的轻弹簧连接在一起，处于自然静止状态。某时刻突然给物体A一个水平向右的速度V₀，同时加一个水平向右的外力F，使物体A保持以V₀的速度做匀速运动，在运动过程中弹簧始终处于弹性限度内。

试求：

（1）A、B间的最小距离是多少？

（2）从开始运动至A、B间达到最小距离的过程中，外力F做了多少功？

解析 （1）物体A和B通过弹簧相互作用，A恒速，B加速，当二者同速时，其间距离最小为L_min。

由结论可知，因相互作用而损失的动能为：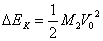

转化为弹簧的弹性势能：

解得：

（2）从开始运动至A、B间达到最小距离的过程中，外力F做功使系统的机械能增加，可知：

例3．在宇宙间某一个惯性参考系中，有两个可视为质点的天体A和B，质量分别为m和M。开始时两者相距为L₀，A静止，B具有沿AB连线延伸方向的初速度V₀。为使B能继续保持匀速直线运动，对B施加一个沿V₀方向的变力F。试求：

（1）A、B间距离最大时的F为多少？应满足什么条件？

（2）从开始到A、B相距最远时力F所做的功？

解析 （1）天体A、B通过万有引力相互作用，当二者同速时，其间距离最大，设为Lmax求解，由结论可知，在A加速的过程中，A增加多少动能，系统就增加多少引力势能，即有，

得：

此时B受到的外力为：

存在最大距离的条件是：

即：

（2）力F所做的功等于系统增加的势能与天体A增加的动能之和，即

例4．宇宙飞船以V₀=10⁴m/s的速度进入均匀的宇宙微粒尘区，飞船每前进S=10³m,要与N=10⁴个微粒相碰。假如每个微粒的质量为m=2×10^-7kg，与飞船相碰后附在飞船上，为使飞船的速率保持不变，每前进S的距离牵引力做功多少？

解析 在飞船不受阻力，只受万有引力的情况下，无需输出功率；当受到尘埃阻力时，需要输出功率来克服阻力做功以维持匀速。尘埃与飞船相互作用，使尘埃的动能增加，即：

则微粒在加速过程中与飞船相互作用而增加的内能跟其动能增加量相同，

即：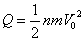

因此，飞船每前进S的距离牵引力做功