谈化学问题中的数学思想
论文关键词:化学,问题,数学思想
一、方程与函数思想
在一些化学问题题中,两个未知量之间遵循一定的函数关系,因此可将相互关联的未知量,运用函数知识加以解决。
例1、将 高锰酸钾粉末加热一段时间后,得到 高锰酸钾粉末加热一段时间后,得到 气体,再将反应后剩余固体投入到足量的浓盐酸中加热,充分反应后又得到 气体,再将反应后剩余固体投入到足量的浓盐酸中加热,充分反应后又得到 气体(其中还原产物只有 气体(其中还原产物只有 ),则 ),则 的值不可能为( ) 的值不可能为( )
A  B B  C C  D D 
解析:设第一阶段高锰酸钾的分解率x(且 ),根据方程式知道: ),根据方程式知道:
 ① ①
用终态分析法知:高锰酸钾在反应过程中由MnO4- Mn2+,得电子,而另一方面氧和氯失去电子生成氧气和氯气,根据电子守恒列出方程:
 ② ②
根据据①和②,可以得到函数关系: ,因为 ,因为 ,所以 ,所以 ,则本题选A 、D. ,则本题选A 、D.
二、极限思想
在解决复杂问题时,根据解题的需要,可采用极端假设法,把问题或过程推向极限,使复杂问题变得单一化、简单化。
例2、在一定条件下,向 密闭容器中充入 密闭容器中充入 和 和 进行反应: 进行反应: ,某时刻测定产物的浓度不可能的是() ,某时刻测定产物的浓度不可能的是()
A、 B、 B、
C、 D、 D、
解析:假设 和 和 完全转化为Z 、W,即向正反应方向“一边倒”,易得出Z 和W的最大值分别为 完全转化为Z 、W,即向正反应方向“一边倒”,易得出Z 和W的最大值分别为 、 、 。对于可逆反应而言,反应物不可能完全转化为生成物,生成物也不可能完全转化为生成物,因此Z 和W物质的量的范围分别为: 。对于可逆反应而言,反应物不可能完全转化为生成物,生成物也不可能完全转化为生成物,因此Z 和W物质的量的范围分别为: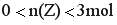  ,则浓度范围分别为: ,则浓度范围分别为: 、 、 。故选C 。故选C
三、分类讨论思想
在一些化学问题中,因为某些待定量的范围不明确,因此必须根据该量的化学意义将其划分为若干部分,然后分别解决,最后归纳出结果,从而达到解决问题的目的。
例3、将 浓度为 浓度为 的 的 溶液滴加到 溶液滴加到 浓度为 浓度为 的 的 溶液中。试推导a 、b关系并计算 溶液中。试推导a 、b关系并计算 的物质的量。 的物质的量。
解析:本题是一道过量且连续反应的综合计算。因此必须挖掘其中可能发生的反应,并从量的关系进行讨论计算。
 ↓ ① ↓ ①
 ② ②
将①式+②得 : ③ ③
⑴当 过量时,将发生反应①,此时因 过量时,将发生反应①,此时因 过量,故有 过量,故有 ,即 ,即 。此时 。此时 沉淀量为 沉淀量为 。 。
⑵当 过量时,且生成的 过量时,且生成的 完全溶解时,会发生反应③ 完全溶解时,会发生反应③
此时因 过量,故有 过量,故有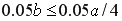 ,即 ,即 ,无 ,无 沉淀。 沉淀。
⑶当 过量,但生成的 过量,但生成的 不完全溶解时,会发生反应①和②两个反应,则有 不完全溶解时,会发生反应①和②两个反应,则有
 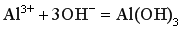 ↓ ↓
  

 
由⑴知 过量时,有 过量时,有 ; 由知⑵ ; 由知⑵ 过量时,且生成的 过量时,且生成的 完全溶解时,有 完全溶解时,有 ,故在⑶的情况下必有 ,故在⑶的情况下必有 ,此时 ,此时 沉淀的量为 沉淀的量为
四、数形结合思想
在化学图像类问题中,应理清其中的物质关系和数量关系,并与图像所反映的变化过程结合起来,实现“数与形”的有机统一,才能轻松解决该类问题。
例4、准确称量6.0g铝土矿样品(含 、 、 、 、 ),放入盛有 ),放入盛有 某浓度的硫酸溶液的烧杯中,完全反应后过滤,向滤液中加入 某浓度的硫酸溶液的烧杯中,完全反应后过滤,向滤液中加入 的 的 溶液,产生的沉淀质量与加入 溶液,产生的沉淀质量与加入 溶液的体积的关系如图所示: 溶液的体积的关系如图所示:
 
①求硫酸的浓度 ②若a=2.3,
则样品中各成分的质量分数
解析:①由图像可知:当加入 溶液时,滤液中过量的硫酸被 溶液时,滤液中过量的硫酸被 中和,且 中和,且  、 、 全部沉淀,溶液中的溶质只有 全部沉淀,溶液中的溶质只有 ,由此建立 ,由此建立 和 和 物质的量的关系: 物质的量的关系: 
即 , ,
②从图像分析:溶解 消耗 消耗 溶液 溶液 ,即 ,即 由 由 得 得 .再由 .再由 得:沉淀 得:沉淀 消耗 消耗 即 即 ,那么沉淀 ,那么沉淀 消耗 消耗 溶液的体积为: 溶液的体积为:
  即 即 .综合分析: .综合分析: ; ; ,则 ,则 , ,  ;进一步计算得 ;进一步计算得 ; ;  ; ; 
五、化归思想
化归即转化、归结,其实质是通过转化实现“化难为易,化繁为简,化多元为一元,化未知为已知”。
例5、由 、 、 、 、 、 、 、 、 、 、 组成的混合物中 组成的混合物中 元素的质量分数为 元素的质量分数为 ,试求氧元素的质量分数。 ,试求氧元素的质量分数。
解析:混合物中共含五种元素,而只知道一种元素的质量分数,使计算陷入困境。但若能抓住“ 、 、 合起来当 合起来当 来考虑”这一组成中的隐含条件,问题便可得到简化。因 来考虑”这一组成中的隐含条件,问题便可得到简化。因 与 与 式量相等,故可将混合物组成转化为“ 式量相等,故可将混合物组成转化为“ ”。 ”。
由 : : =1:1 得: =1:1 得:  : : = 3:4 = 3:4
 : : = 3:4, = 3:4,  = = ,即钠、氢、镁三元素总质量分数: ,即钠、氢、镁三元素总质量分数: = =  ,则氧元素质量分数为: ,则氧元素质量分数为:

总之,化学计算是化学原理与数学方法的有机统一,只有从化学问题中准确提取出数学信息,并将其抽象为数学模型,再结合化学原理,选择恰当的数学方法加以解决。
|


