| 论文摘要:随着当前大学生毕业就业形势变化,大学生毕业后是就业还是考研的问题引起了广泛关注。本文针对这一问题,运用层次分析法构建大学生毕业去向模型,分析各个因素的影响。
论文关键词:金融危机,层次分析法,大学生毕业去向
1.问题的重述
1)问题提出的背景
最近几年,我国大学毕业就业产生不少新变化。首先,我国本土大学生面临国际联合办学机构竞争。近几年来,我国高教市场逐步向国外资本开放,各种形式外国教育机构的进入,产生了更多类型的人才培养机构,他们不但提供了人才短期培训,不少教育机构还与国内大学进行联合办学,这种全新人才培养模式直接挑战了中国本土高校人才培养模式,对我国本土高校大学生就业增强了不少的竞争对手。其次,人才市场更加偏重“好”专业。所谓的“好”专业或“热”专业,是指当前就业市场较紧缺的专业。第三,金融危机直接影响行业就业,并可能引发更大规模的就业冲击。因美国次贷危机而引发的国际社会金融海啸导致了金融机构的连锁性破产,引发了金融行业的裁员风潮,这更给就业产生了巨大冲击。
2)要解决的问题
面对诸多挑战与机遇,大学生毕业后主要有五种选择方案:继续考研深造、考公务员、到企业工作、自主创业和待业。那么有哪些因素影响着大学生的选择,影响程度有多大,主要影响因素是什么呢?这是本文要讨论的问题。
2.问题的分析
大学生毕业去向有继续考研深造(在扩大本科招生规模的情况下,硕士研究生的招考比例也随之增加,它已经成为许多同学努力的方向。)、考公务员(公务员一直被认为是“铁饭碗“,也是大学生选择的方向。)、到企业打工(进入各类国营、民营、三资企业打工,从事专业技术或营销等工作,在实践中段练自己。)、自主创业(当前形势下,随着我国对当代大学生自主创业的支持和一系列优惠政策的出台,以及大学生自主创业日益高涨的热情,大学生逐渐把自主创业作为就业的一条主要途径。)和待业(应届大学毕业生考研或公务员落榜继续再考,或者等待机遇就业。由于受录取人数和岗位数量的限制,不可能所有的大学生都上榜,因此,相当一大批大学生选择继续考研或公务员。[1])五种,而现在大学生面临选择的时候需要考虑的因素有个人因素、专业因素和社会因素三个方面,个人因素主要包括个人兴趣、个人能力和家庭经济情况;专业因素包括专业是否有对口工作和专业冷热程度;社会因素有人才需求比例和社会福利程度等。这些因素都影响着大学生做出选择,为了帮助大学生能够更好的做出选择本文就以上因素用层次分析发[1]分析各个因素对大学生决策的影响程度,本文建立了层次结构模型-----主要分为四层(最高层为目标层,其次为准则层和子准则层,最后为方案层)分析各个因素在大学生毕业去向的选择中占的比重。
3.模型的建立及求解
3.1模型的分析
层次分析法[2]的的基本思路与人们对复杂的决策问题的思维判断过程大体一致,现将问题分为若干层次,最高层为目标层,这一层中只有一个元素,就是问题要达到的目标或理想的结果;中间层为准则层,层中的元素是为实现目标所采用的措施、政策、准则等,准则层可以不止一层;最底一层为方案层,这一层包括为了实现目标可供选择的方案。
对于大学生毕业去向问题本文分为四个层次:(1)最高层即目标层为大学生毕业去向选择,记为 ;(2)中间层包括准则层和子准则层。准则层记为 ;(2)中间层包括准则层和子准则层。准则层记为 ,包括三个准则:个人因素,记为 ,包括三个准则:个人因素,记为 ;专业因素,记为 ;专业因素,记为 ;社会因素,记为 ;社会因素,记为 。子准则层记为 。子准则层记为 ,包括七个指标:个人兴趣,记为 ,包括七个指标:个人兴趣,记为 ;个人能力,记为 ;个人能力,记为 ;家庭经济情况,记为 ;家庭经济情况,记为 ;专业是否有对口工作,记为 ;专业是否有对口工作,记为 ;专业冷热,记为 ;专业冷热,记为 ;人才需求比例,记为 ;人才需求比例,记为 ;社会福利,记为 ;社会福利,记为 ;(3)最底层为方案层,即大学生毕业去向有哪些选择,记为 ;(3)最底层为方案层,即大学生毕业去向有哪些选择,记为 ,分为五个方案:考研深造,记为 ,分为五个方案:考研深造,记为 ;考公务员,记为 ;考公务员,记为 ;到企业打工,记为 ;到企业打工,记为 ;自主创业,记为 ;自主创业,记为 ;待业在家,记为 ;待业在家,记为 。在层次结构中,各层指标及方案都称为元素,非最低层的每个元素支配着与它有关的下一层元素。 。在层次结构中,各层指标及方案都称为元素,非最低层的每个元素支配着与它有关的下一层元素。
3.2模型的建立与求解
(1)建立方案评价的递阶层次结构模型
(2)构造比较判断矩阵
设以 为比较准则, 为比较准则,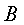 层次各因素的两两比较判断矩阵为 层次各因素的两两比较判断矩阵为 ;类似地,以每一个 ;类似地,以每一个 为比较准则, 为比较准则, 层次各个因素的两两比较判断矩阵为 层次各个因素的两两比较判断矩阵为 ; ;
对于总目标 ,有 ,有
|

|

|

|

|

|
|

|
1
|
2
|
4
|
0.557
|
|

|
1/2
|
1
|
3
|
0.320
|
|

|
1/4
|
1/3
|
1
|
0.123
|
对于准则 ,有 ,有
|

|

|

|

|

|
|

|
1
|
1/5
|
1/3
|
0.110
|
|

|
5
|
1
|
2
|
0.581
|
|

|
3
|
1/2
|
1
|
0.309
|
对于准则 ,有 ,有
对于准则 ,有 ,有
 
所以正互反矩阵的最大特征值 为 为 ,对应的特征向量为 ,对应的特征向量为
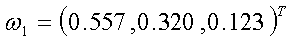
其他比较判别矩阵的权重与最大特征值与上面的方法一致,此略。
(3)层次但排序及其一致性检验
对于上述各比较判断矩阵,可用 数学软件求出其最大的特征值及其对应的特征向量,将特征向量归一化后,即可得到相应的层次排序的相对重要性权重向量,以及一致性指标 数学软件求出其最大的特征值及其对应的特征向量,将特征向量归一化后,即可得到相应的层次排序的相对重要性权重向量,以及一致性指标 和一致性比例 和一致性比例 ,如下表: ,如下表:
|
矩阵
|
层次单排序的权重向量
|

|

|

|

|
|

|

|
3.019
|
0.0095
|
0.58
|
0.016
|
|

|

|
3.004
|
0.002
|
0.58
|
0.003
|
|

|

|
2
|
0
|
0
|
0
|
|

|

|
2
|
0
|
0
|
0
|
由表可见,所有4个层次但排序的 的值均小于 的值均小于 ,符合满意一致性需求。 ,符合满意一致性需求。 1/2 1 2 下一页 尾页 |


