论文摘要:在某型高炮随动系统的测试中,待测信号有非时变信号和时变信号两种。本文根据这两种信号的特点,对比分析了一阶差分法、多项式逼近法和线性回归法,对每种方法的处理方式进行了研究,得到了以上两种信号的处理方法。
论文关键词:数据处理,多项式逼近法,线性回归法
引言
根据某型高炮随动系统测试数据的特点,一般可分为非时变数据(即被测物理量是常数的多次测量数据)和时变数据(包括谱数据)两种,视其情况不同需分别进行处理。
由于对非时变数据可以实施反复测量,剔除粗差以降低外界干扰因素对测量结果的影响,因此只需要考虑排除干扰值,而不需要用预测值取代异常值,从而使数据处理过程简化。
对时变数据,不易采用反复检测以检验测试结果的正确性。因此在对全部数据复原时,不仅必须把因受到干扰而产生的虚假数据检测出来,还必须补上一个合理的数值,这一数值是通过预测方法来得到的,我们假设测量数据序列为 ,相应时刻分别为 ,相应时刻分别为 ,预测合理值的方法主要有以下三种: ,预测合理值的方法主要有以下三种:
1一阶差分法
假设已知k时刻之前的两个采样点的值 、 、 ,则: ,则: 。 。 为 为 的预测值。采用这种方法,一般数据的采样频率应是物理量变化最高频率的十倍以上,才不至于使预测误差过大。这种方法满足于很多测试情况,尤其对于具有冲击干扰的对象来讲,更具有简单、实用的优点。 的预测值。采用这种方法,一般数据的采样频率应是物理量变化最高频率的十倍以上,才不至于使预测误差过大。这种方法满足于很多测试情况,尤其对于具有冲击干扰的对象来讲,更具有简单、实用的优点。
2多项式逼近法
当采样频率低于物理量变化最高频率的十倍时,可用前三点构成二次曲线来进行预测,设测量序列的前三点为 , , , , 满足二次曲线方程: 满足二次曲线方程: ,则有: ,则有:



求得待定系数 , , , , ,则 ,则 时刻的预测值为: 时刻的预测值为:

这种预测方法在采样频率为物理量最高频率六倍以上时,具有足够精度。对于采样频率更低的数据,可采用更高次曲线来预测。
3线性回归法
上述两种方法适用于测量误差很小的情况,对于测量误差较大的数据,则一般采用线性回归算法,即利用前几个数据来拟合直线或曲线,进行预测。
还有,当两个物理量X和Y之间有一定的函数关系,但具体的函数关系或函数中的某些参数需通过实验检测有限个数据来确定最终的函数关系时,利用线性回归预测算法也是行之有效的。
在这种方法中,存在用多少次的曲线来拟合与利用前面多少个数据点的问题,这都是需要根据采样频率及被测量数据的特点来适当选择的。
在确定预测算法之后,就需要选定误差窗口W,以便根据 是否大于W,来判断 是否大于W,来判断 是否为干扰值,误差窗口的选择一般需经以下两个步骤: 是否为干扰值,误差窗口的选择一般需经以下两个步骤:
2.1W的选取范围的确定
这项工作进行时,应十分谨慎,如果W过大,异常数据可能剔出不掉;而W过小,则可能剔出正常数据,因而都可能得不到高质量的测量结果。
假定预处理的一维数组为 ,然后利用以下公式构成一个新的数组 ,然后利用以下公式构成一个新的数组 。 。

把由此得到的数组由小到大的顺序排列,则得到有序数组 , , … … , , ,其中最小值为 ,其中最小值为 ,最大值为 ,最大值为 。将其看作W的离散数列,只取整数 。将其看作W的离散数列,只取整数 ,由此就把W的取值范围限定为: ,由此就把W的取值范围限定为:

2.2W值的计算
可以通过不同的计算方法来寻求合理的W。
(1)固定系数法
以最小的 为准,选取 为准,选取 ,一般可选 ,一般可选 ,这种方法对变化不很复杂的曲线特别有用。 ,这种方法对变化不很复杂的曲线特别有用。
(2)求平均值法
把数组的 当作测量W而得到的数组,寻求偏差最小的数组,然后再求它们的平均值。 当作测量W而得到的数组,寻求偏差最小的数组,然后再求它们的平均值。
根据不同的情况,可分别选用狄克逊准则,肖维勒准则及莱因达准则等来剔除粗差。
将干扰值剔除(即找到最小偏差数组)后,求其平均值,则可得到W。
设 , , … … , , 为剔出干扰值后得到的新数组,则: 为剔出干扰值后得到的新数组,则:

(3)选择多个W
上述方法适用于数据范围不宽的情况,如果数据范围很宽,有时需要选用不同的W值以适应不同的要求。
设窗口数组 , , ,则得到三个W值为: ,则得到三个W值为:



当 , , 或 或 时,则选 时,则选 。因此,在这三种情况下,就转化为唯一的W问题,使处理过程大大简化。 。因此,在这三种情况下,就转化为唯一的W问题,使处理过程大大简化。
假如不满足以上三个条件,则已知 、 、 ,而 ,而

用此三个W,进行数据处理,得到相应得三个数组:
 ;用 ;用 处理 处理
 ;用 ;用 处理 处理
 ;用 ;用 处理 处理
再把这三个数组的对应点进行比较,取中间值构成新的数组 ,一般 ,一般 就可作为最终结果,有时为了最大限度地保持原 就可作为最终结果,有时为了最大限度地保持原 的关系进行点—点比较,以构成新数组 的关系进行点—点比较,以构成新数组 , , 的构成方法如下: 的构成方法如下:
if

else
当 时,则认为 时,则认为 为虚假点,并用预测值 为虚假点,并用预测值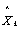 取代 取代 。在具体应用时,还应注意以下几点: 。在具体应用时,还应注意以下几点:
(4)起始点的选择
有时所采用的第一点或第二点就是虚假点,因此,一开始必须寻找满足预测关系得连续三点,即满足

这三点满足线形外推关系,因此是合理的起点。 1/2 1 2 下一页 尾页 |


