论文摘要:运用物理学的方法和微积分的知识来建立数学模型,借促MATLAB软件,得到结果:在第60秒引擎刚关闭时,火箭的高度为9317.8米,速度为274m/s,加速度为132.7931m/s ;火箭达到最高点的时间为70.2s,高度为14604m.k的值估计为0.4904.
论文关键词:火箭升空,牛顿第二定律,软件
一、问题重述
火箭的质量为300千克(kg),携带900千克燃料并以15kg/s速率燃烧而产生恒定40000牛顿推力.同时受与速度的平方成正比,比例系数为k的空气阻力,在t时间时高度x(t),速度为v(t),取重力加速度g为9.8m/s.
二、问题假设
1.空气的阻力f与速度平方v成正比,比例系数为k;
2.燃料以15千克/秒的速率燃烧,并产生40000牛顿的恒定推力;
3.重力加速度g为9.8m/s;
4.火箭本身的质量为m,剩下燃料的质量为m;
5.火箭运行的高度x(米)与时间t(秒)和速度v(米/秒)对应的关系,x(t)为火箭在时t的高度测有一组数据如下:
三、模型求解
1.建立模型
由物理学可知,在t时刻,火箭和燃料的质量为1200-15t;重力产生的阻力为(1200-15t)×9.8;空气阻力为kv;那么,由牛顿第二定律可得
 ;0 ;0
|
t
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
|
x
|
1070
|
1270
|
1480
|
1700
|
1910
|
2140
|
2360
|
2600
|
2830
|
3070
|
3310
|
|
v
|
190
|
200
|
210
|
216
|
225
|
228
|
231
|
234
|
239
|
240
|
246
|
----------------------------------------------------------------------
*科研项目:安康学院大学生科技创新项目(2009AKXYDXS06).
 t>60 t>60
由 ,可得到 ,可得到 ;0 ;0 (1) (1)
 t>60(2) t>60(2)
 (3) (3)
2.模型求解
当0时,令a=dv/dt.由t和v的对应关系在matlab中编程以及给出的公式
t=10:20;
v=[195228231234239240246];
fori=3:10
a(i)=(1/12)*(v(i-2)-8*v(i-1)+8*v(i+1)-v(i+2));
end
a=[10107.75007.6676.252.52.8334.33332.753.58.5]
将a的值代入(3)中,在matlab中可求得k=0.4904.
在(1)式中,由 ,得 ,得
 (4) (4)
求解过程,编写m文件如下:
---------------------------------------------------------------------------------------------------------------
functionxdot=wf(t,x)
xdot=zeros(2,1)
xdot(1)=x(2)
xdot(2)=[28240+147*t-0.4904*x(2).^2]/(1200-15*t)
在命令窗口中执行:
xspan=0:1:60;x0=[00]';
[t,x]=ode45('wf',xspan,x0);
plot(t,x)
结果为:
ans=1.0e+004*
----------------------------------------------------------------------------------------------------------------
Columns1through10
………………
Column61
1.3807
0.0274
故在t=60s时,x(t)=1.3807*10,v(t)=0.0274*10m/s.
此时关闭引擎,t=60s,火箭推力为0时只受空气阻力与自身重力作用m=300kg,所以
加速度 . .
火箭关闭引擎后(t>60)
 ,转化为 ,转化为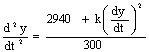
设 ,得微分方程组 ,得微分方程组
 , , (5) (5)
求解过程,编写m文件如下:
----------------------------------------------------------------------------------------------------------------------------------
functionact=wf(t,y)
act=zeros(2,1);
act(1)=y(2);
act(2)=-[0.4904*y(2).^2/300+9.8]
在命令窗口中执行:
vspan=60:0.2:74;
[t,y]=act(‘wf’,vspan,[13807274]);
输出的结果:
ans=1.0e+004*
---------------------------------------------------------------------------------------Columns1through10
………………
1.4604
0.0000
由输出的结果可知道:当t=70.2时,y(1)=14604,y(2)=0,即此时的速度v=0m/s;而且此时火箭达到最大高度.
所以火箭升到最大高度所花的总时间T=70.2s.关闭引擎后,火箭上升到最大高度H=14604m.至此,问题得到解决.
参考文献
1 阳明盛、熊西文,MATLAB基础及数学软件.大连:大连理工大学出版社,2003.8.
2 夏玮、李朝晖,控制系统仿真与实例详解.北京:人民邮电出版社,2008.10.
3 胡祥青,大学物理.北京:北京师范大学出版社,2005.5. |


