论文导读::将裂缝损伤简化成矩形凹槽,采用delta函数表示简支梁的裂纹损伤位置,得到了全梁范围内截面转动惯量和单位长度质量的表达式,建立了局部裂缝损伤简支梁的横向自由振动方程。利用摄动方法给出了裂纹摄动项的一般表达式,根据摄动项和完整梁都同时满足边界条件的特点,将一阶和二阶摄动项都表示成完整梁模态的线性组合,结合delta函数的性质,最终获得了受损简支梁的特征值和模态振型的解析表达式。最后,通过数值计算得到结构模态参数,对比了一阶摄动和二阶摄动对计算结果的影响,分析了不同阶固有频率和模态曲率的变动量,为简支梁的损伤监控和检测提供了理论依据。
论文关键词:裂纹损伤,简支梁,摄动方法,模态分析方法,曲率模态
1 引 言
随着使用年限的增加,结构的强度和刚度等性能必然会下降,如果出现损伤,结构的动力特性如固有频率、固有振型和模态阻尼都会产生变化,通过研究结构动力特性的变化来检测和检控结构的损伤是目前一个重要研究课题[1]。文[2]根据结构动力学理论,以结构损伤后系统各种模态参数的改变作为特征标识量对损伤进行诊断,虽然效果很好,但主要适应于严重损伤的情况,当结构局部受损且程度较低时,结构模态参数的改变甚微,这时无法从结构固有频率或模态阻尼的改变来判断结构是否存在损伤[3,4],目前,国内外众多学者比较认可的是根据模态曲率的特性对低程度损伤进行检测,并已进行了大量的相关研究:文[5]研究指出,曲率模态对局部参数变化较传统的模态分析方法更为敏感,在结构的损伤检测及损伤定位中具有优越性;文[6]对实桥的损伤进行了检测摄动方法,并根据实测数据采用曲率模态分析对损伤进行了分析但上述研究主要集中于数值模拟,关于损伤对曲率模态的影响的研究报道很少。文[7]利用一阶摄动方法给出了摄动项的一般表达式,推导了受损悬臂梁的固有频率和模态振型的解析表达式,并就结构损伤对位移模态和曲率模态的影响作了分析和研究。
目前关于简支梁裂纹损伤的相关理论研究较少报道,本文将裂纹损伤展开成二阶摄动,得到了固有频率、模态振型和模态曲率的解析式,通过数值计算,对比了一阶摄动和二阶摄动对计算结果的影响,分析了不同阶的模态曲率的变动量。
2 受损简支梁的结构模型
受损简支梁的简化模型如图1所示,梁的截面为矩形,宽度和高度分别为b和h,梁长为l,在简支梁底部xd处存在一处裂纹损伤,裂纹简化成矩形凹槽,裂纹的宽度和深度分别为?l和hd。

图1 底部存在一处损伤裂缝的简支梁模型
Fig.1 Structuralmodel of a simple beam with a damaged crack at the bottom
在损伤部位,梁的截面转动惯量和单位长度梁质量的表达式分别为
 (1) (1)
 (2) (2)
令 , , , , ,引入delta函数 ,引入delta函数 ,将上式展开,因为 ,将上式展开,因为 ,略去三阶小项O(ε3),则全梁范围内的截面转动惯量和单位长度质量可分别表示成 ,略去三阶小项O(ε3),则全梁范围内的截面转动惯量和单位长度质量可分别表示成 的形式 的形式
 (3) (3)
 (4) (4)
本文主要研究固有频率和模态振型等结构动力参数,故不考虑体力和外部荷载作用,于是梁的自由振动微分方程为[8]
 (5) (5)
式中, 为材料的弹性模量, 为材料的弹性模量, 为梁中性面上各点的横向位移中国学术期刊网。 为梁中性面上各点的横向位移中国学术期刊网。
将式(3)和(4)代入式(5)可得:
 (6) (6)
简支梁的边界条件为
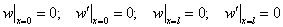 (7) (7)
式(7)的通解可表示为 阶主振动的叠加 阶主振动的叠加
 (8) (8)
式中, 、 、 和 和 分别为梁的第 分别为梁的第 阶模态振型、特征值和相位角, 阶模态振型、特征值和相位角, 满足正交性。 满足正交性。
3 受损简支梁的模态振型和模态曲率
由式(8)代入(6),根据模态 的正交性,对于任意的 的正交性,对于任意的 阶模态,都满足 阶模态,都满足
 (9) (9)
考虑到梁的局部微小损伤摄动方法,因而 、 、 都是很小的量,损伤后结构的特征值和模态振型是损伤前的一个微小扰动,根据二阶摄动理论,损伤后的特征值和模态振型可表达成[9] 都是很小的量,损伤后结构的特征值和模态振型是损伤前的一个微小扰动,根据二阶摄动理论,损伤后的特征值和模态振型可表达成[9]
 (10) (10)
 (11) (11)
式中, 和 和 是完整梁的特征值和模态振型, 是完整梁的特征值和模态振型, 和 和 是裂纹损伤引起的特征值和模态振型的一阶摄动量, 是裂纹损伤引起的特征值和模态振型的一阶摄动量, 和 和 是裂纹损伤引起的特征值和模态振型的二阶摄动量。 是裂纹损伤引起的特征值和模态振型的二阶摄动量。
将(10)和(11)代入式(9),按系数项 和 和 展开,略去小项O(ε2),整理后可得 展开,略去小项O(ε2),整理后可得
 : :  (12) (12)
 : : (13) (13)
 : :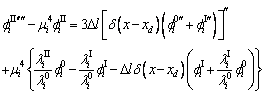
(14)
式中, 为完整梁第i阶振型的波数。 为完整梁第i阶振型的波数。
 (15) (15)
完整梁的 、 、 和固有频率 和固有频率 的解答可直接根据文献[8]由式(12)求得 的解答可直接根据文献[8]由式(12)求得
1/2 1 2 下一页 尾页 |


