论文摘要:为了减少在轧钢生产中的浪费问题,我们把不符合标准的整根废钢,再度开发利用,或者是在生产中尽量减少被裁减钢材的长度,使得整条钢材得到最大利用,运用概率论知识,建立浪费模型,并求出最优解。在前人所做的特殊问题讨论上,推广到一般情况。
论文关键词:轧钢,均值,方差,微分法
一、问题的提出
用连续轧钢方法制造钢材时要经过两道工序,第一道是粗轧(轧钢),形成钢材的雏形;第二道是精轧(冷拔),得到规定长度的钢材。粗轧时由于设备、环境等方面随机因素的影响,钢材冷却后的长度大致上呈正态分布,其均值可以在轧制过程中由轧机调整,而其均方差则是由设备的精度决定的,不能随意改变。精轧时把多出规定长度的部分切掉,但是如果发现粗轧后的钢材已经比规定长度短,则整根报废。精轧设备的精度很高,轧出的成品才可以认为是完全符合规定长度要求的,根据轧制工艺的要求,要在成材规定长度和粗轧后钢材长度的均方差已知的条件下,确定粗轧后钢材长度的均值,使得当轧机调整后进行粗轧,再通过精轧以得到成品材时的浪费最少。显然,应该综合考虑这两种情况,在第二种情况下我们在考虑两套方案或多套方案,可以满足不同规格,使得总的浪费最小。
二、符号说明
 ——粗轧后钢材长度 ——粗轧后钢材长度
 —— —— 的平均值 的平均值
 —— —— 的均方差 的均方差
 —— —— 的概率密度 的概率密度
 ——钢材总的浪费长度 ——钢材总的浪费长度
 ——成品材的规定长度 ——成品材的规定长度
 ——成品材的规定长度备用方案1 ——成品材的规定长度备用方案1
 ——成品材的规定长度备用方案2 ——成品材的规定长度备用方案2
 ——成品材的规定长度备用方案3 ——成品材的规定长度备用方案3
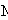 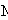
三、模型假设
1.不考虑钢胚的质量问题,钢胚的规格都统一;
2.精轧的设备精度很高,认为它没偏差;
3.不考虑环境温度对钢材热胀冷缩的影响;
四、问题分析
在实际钢材生产中,粗轧后钢材长度记作 , , 是均值 是均值 和方差 和方差 的正态随机变量, 的正态随机变量, 的概率密度记作 的概率密度记作 ,其中 ,其中 已知, 已知, 是待确定的值. 是待确定的值.
当成品材的规定长度 、 、 和 和 给定后,记 给定后,记
 的概率为 的概率为 ,即 ,即 ; ;
 的概率为 的概率为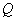 ,即 ,即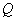   ; ;
 的概率为 的概率为 ,即 ,即 。 。
在精扎时,轧制过程中的浪费由四部分构成,
一是当 时,精轧时要切掉长 时,精轧时要切掉长 ; ;
二是当 时,裁掉钢材长 时,裁掉钢材长 ; ;
三是当 时,裁掉钢材长 时,裁掉钢材长 ; ;
四是当 时,整根钢材报废,长度为 时,整根钢材报废,长度为 。 。
在生产中要计算好适当的 使得浪费的钢材最少、成才最多,关键是要选择合适的目标函数,并用已知的和待确定的量 使得浪费的钢材最少、成才最多,关键是要选择合适的目标函数,并用已知的和待确定的量 , , , , ,s,m把目标函数表示出来。一般我们可以想到,直接将上面分析的四部分浪费之和作为目标函数,于是容易得到总的浪费长度为 ,s,m把目标函数表示出来。一般我们可以想到,直接将上面分析的四部分浪费之和作为目标函数,于是容易得到总的浪费长度为
 
利用
 , ,
 , ,
 , ,
 , ,
 , ,
代入 式,可化简为 式,可化简为
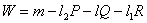 
 中的 中的 是每轧一根钢材浪费的平均长度。设共粗轧了 是每轧一根钢材浪费的平均长度。设共粗轧了 根钢材 根钢材  很大 很大 ,所用钢材的总长为 ,所用钢材的总长为 , , 根中可以轧出成品材的只有 根中可以轧出成品材的只有 (我们可以把一根长 (我们可以把一根长 的成品材可以看作是 的成品材可以看作是 根长为 根长为 的成品材,以此类推又可以把一根长 的成品材,以此类推又可以把一根长 的成品材可以看作是 的成品材可以看作是 根长为 根长为 的成品材),成材品的总长为 的成品材),成材品的总长为 , ,
于是共浪费的总长度为 ,平均每粗轧一根钢材浪费的长度为 ,平均每粗轧一根钢材浪费的长度为
 
与 式相同。轧钢的最终产品是成品材,浪费的多少不应以每粗轧一根钢材的平均浪费量为标准,而应该用每得到一根成品材浪费的平均浪费来衡量.为了将目标函数从前者改成后者,只需将 式相同。轧钢的最终产品是成品材,浪费的多少不应以每粗轧一根钢材的平均浪费量为标准,而应该用每得到一根成品材浪费的平均浪费来衡量.为了将目标函数从前者改成后者,只需将 式左端分母改为成品材总数 式左端分母改为成品材总数 即可。 即可。
五、模型建立与求解
我们由以上问题分析得出的结论可得。将每得到一根成品材浪费钢材的平均长度为目标函数.由以上的分析可知目标函数为
 
因为 、 、 、 、 是已知常数,所以目标函数可等价地只取上式右端第一项,即 是已知常数,所以目标函数可等价地只取上式右端第一项,即
 
式中 , , , , 表示概率 表示概率 , ,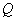 , , 是 是 的函数。 的函数。
下面求 使得 使得 达到最小。对于表达式 达到最小。对于表达式
 , , , , , , , ,
作变量代换
 , , , , , , , , , ,
则 式可表达为 式可表达为
 , ,
其中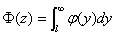 , , 是标准正态变量的密度函数。 是标准正态变量的密度函数。
利用微分法解函数极值问题时,我们还必须注意到 ,可以推出 ,可以推出 的最优解 的最优解 必须满足方程 必须满足方程 , ,
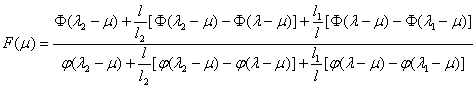
当 、 、 、 、 、 、 已知,即 已知,即 、 、 已知时, 已知时, 可根据函数值 可根据函数值 、 、 制成表格,由表格可以得到方程的最优根 制成表格,由表格可以得到方程的最优根 ,再代回上式即得到 ,再代回上式即得到 的最优解 的最优解 。 。
六、结论
本模型用于轧钢生产中的规格制定以减少浪费。在实际生产当中,所需的钢材是多种规格的例如 ,按照以上方法我们可以推广到更多的规格。因为钢材在具有延展性和热胀冷缩的特点并且热胀冷缩系数比较大,生产钢材的也会有热胀冷缩变化和材料疲劳现象导致在大规模生产时产生误差。另外,我们可以考虑把短于预定规格的钢材,裁切成更小的规格,以减少整根报废的可能性。把长于预定规格的钢材,减少裁切的长度,形成大规格的钢材,以减少因为裁切而浪费的钢材。 ,按照以上方法我们可以推广到更多的规格。因为钢材在具有延展性和热胀冷缩的特点并且热胀冷缩系数比较大,生产钢材的也会有热胀冷缩变化和材料疲劳现象导致在大规模生产时产生误差。另外,我们可以考虑把短于预定规格的钢材,裁切成更小的规格,以减少整根报废的可能性。把长于预定规格的钢材,减少裁切的长度,形成大规格的钢材,以减少因为裁切而浪费的钢材。
参考文献
1 姜启源.数学模型[M].北京:高等教育出版社,1993.
2 李贤平.概率论基础[M].北京:高等教育出版社,2001
3 朱建青,张国梁.数学建模方法[M].郑州:郑州大学出版社,2003
4 蔡述健,宁德师专学报(自然科学版).宁德 352100 |


