农业固定资产投资与农业经济增长关系的研究_格兰杰因果检验-论文网

论文摘要：通过对1985—2008年全国农业固定资产投资和农业经济增长的时间序列进行协整检验、误差修正模型、格兰杰因果检验以及灰色关联度分析。结果表明：农业固定资产投资和农业经济增长存在协整和格兰杰因果关系，且关联度紧密；农业经济增长会促进农业固定资产投资的增加，但由于农业固定资产投资具有滞后效应的特性，它在投资达到一定年限后，才会对农业经济起促进作用，且非常显著。
论文关键词：农业固定资产投资,农业经济增长,协整检验,格兰杰因果检验,灰色关联度

通讯作者与地址：邱福林，湖北省武汉市华中师范大学政治学研究院08政府经济学，430079

联系方式：、qqlin8354@yahoo.com.cn

一、引言

中国作为一个农业大国，农业的持续稳定发展是国民经济稳定发展的重要基础。近年来许多学者从科研、财政支农、技术进步、人力资本、农村经济制度等方面对农业经济增长进行实证研究，但对农业固定资产投资（AIFS）与农业经济增长（AEG）关系的研究仍停留在理论和规范研究上。倪心一通过对美国、日本、印度、巴西等国的农业固定资产投资发展历程进行研究对比，得出农业固定资产投资与农业经济增长之间的关系，并指出农业固定投资在全社会固定资产投资中应具有的规模水平。雷锡禄等从我国农业固定资产投资的发展历程指出农业固定资产投资对农业经济增长的重要性，并指明我国农业固定资产投资的发展战略。国外的农业发展史也表明增加农业固定资产投资，是改变农业生产条件，提高农业综合生产能力，实现农业持续稳定协调发展的重要物质基础。目前我国农业固定资产投资主要是以基础设施建设为主，随着国家对三农问题的重视，国家财政不断加大对农业固定资产投资的倾斜。通过绘制1985—2008年全国农业固定资产投资与农业经济增长关系的散点图（因篇幅大，省略），可以发现，随着农业固定资产投资的增加，农业经济也随之不断增长，但两者是否存在长期的均衡和因果关系呢？这正是本文所要研究的内容，通过对两者关系做实证研究能为有关部门制定政策提供依据，对促进农业发展而言也更具现实意义。

二、数据采集与研究方法

分别选取全国农林牧渔的固定资产投资总额和农林牧渔经济总量作为农业固定资产投资和农业经济增长的指标，基于1985—2008年的数据并建立时间序列。全部数据来源于相关年的中国统计年鉴，为了避免数据时间序列中的异方差影响，对所有数据进行对数处理，并分别用LAIFS和LAEG来表示取自然对数后的农业固定资产投资和农业经济增长。

研究农业固定资产投资与农业经济增长的相关关系，需建立两者的回归方程。为防止回归方程出现伪回归现象，需要先做协整检验，以保证方程的有效性。而在分析两者是否具有

协整关系之前，首先要进行序列的单位根检验，只有序列是同阶单整的平稳序列才有可能存在协整关系。如果两者存在协整关系，则进行误差修正模型分析，去除残差的相关性。最后通过格兰杰因果检验，分析两者之间是否存在格兰杰因果关系。以上检验分析将采用计量分析软件Eviews5.0来完成。

基于灰色系统理论计算出两者的关联度。两个系统或因素之间关联性大小的度量称为关联度，灰色关联分析的基本思路是根据序列曲线几何形状的相似程度来判断其联系是否紧密，曲线越接近，相应序列之间关联度就越大，反之越小。它的分析过程一般包括如下过程：在原有数据基础上，计算关联系数，求关联度，而这些过程将采用灰色系统分析软件DPS9.50来完成。

三、实证研究与结果分析

（一）平稳性检验

如果一个时间序列的均值或自协方差函数随着时间而改变，那么这个序列就是非平稳时间序列。一般地，如果时间序列经过d次差分达到平稳，则称为d阶单整序列。本文采用单位根检验中的ADF检验。如果检验t统计值小于显著性水平下的临界值，那么拒绝原假设，认为序列不存在单位根，是平稳的；反之，则认为序列存在单位根，是非平稳的。分别对序列LAIFS和LAEG进行单位根检验，结果见表1。检验结果表明，序列LAIFS和LAEG在二阶差分后，1%的显著性水平下均拒绝零假设，即为二阶单整序列，此时满足协整检验前提，说明两者可能存在长期的协整关系。

表1农业固定资产投资和农业经济增长序列的单位根检验结果

说明：（1）检验类型中的c、t和k分别表示常数项、趋势项和滞后期数；（2）i表示一阶差分，ii表示二阶差分。

（二）协整检验

协整检验的前提是两个变量均为单整变量，只有当它们的单整阶相同时，才可能具有协整关系。当两个变量协整时，则它们之间存在着一个长期稳定的比例关系；反之，当两个变量不是协整的，则它们之间就不存在着一个长期稳定的关系。为了确定LAIFS和LAEG之间是否具有协整关系，采用EG两步法进行检验：（1）对序列进行OLS回归；（2）对回归后的残差进行平稳性检验，若其残差是平稳的，即说明两个变量之间是协整的，否则就不具有协整关系。

首先建立回归方程：

其中α、β为待定参数，是LAEG的估计值，应用普通最小二乘法，估计得α=-12.95306，β=1.841891。则所得方程为：

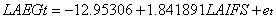
（-11.53972）（15.98266）

模型残差估计值为：

R2=0.920705，AdjustedR-squared=0.917101，DW=0.238689，AIC=1.365803

从模型的估计结果来看，可决系数为0.9207，并且均通过了t检验和F检验，说明模型的拟合效果很好。

 1/3    1 2 3 下一页 尾页