
其中 和 和 分别代表duplication matrix和它的Moore-Penrose逆。 分别代表duplication matrix和它的Moore-Penrose逆。
(二)模型参数估计
将参数向量记作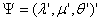 金融论文,其中 金融论文,其中 
 。 。 代表矩阵 代表矩阵 中的所有参数。 中的所有参数。
1.ML估计
满足NMN(k)-GARCH模型的 的对数似然函数为 的对数似然函数为
 (7) (7)
则 的估计 的估计
2.EM算法
在EM框架中, 被视为是不完全的,因为我们不知道每个观测值是来自混合结构中的第几个成分。而这个信息通过一个隐变量 被视为是不完全的,因为我们不知道每个观测值是来自混合结构中的第几个成分。而这个信息通过一个隐变量 给出,其中 给出,其中
 。则对数似然函数可表示为 。则对数似然函数可表示为
 (8) (8)
由于 不可观测,因此我们分两步求解。 不可观测,因此我们分两步求解。
E-step:假定 已知且为 已知且为 ,计算 ,计算 的条件期望,即 的条件期望,即
 (9) (9)
然后用上式代替(7)中的 ,这样对数似然函数就成为: ,这样对数似然函数就成为:
 (10) (10)
M-step:求出使(10)式最大化的 ,记作 ,记作 。 。
上述的E-step和M-step反复迭代直到收敛,即可得到 的最终估计值。 的最终估计值。
实际上,随着k的增大,待估参数的数量会变得异常大,估计起来非常麻烦且费时,因此为了简化待估参数的结构,通常选取k=2,本文也这样选取。另外,文献[7]中的实证研究表明MLE和EM算法估计出来的参数结果无显著差异,因此本文采用MLE方法估计模型参数。
(三)广义似然比检验
由于正态总体在实际中工作中最常见,数学处理上也比较成熟,故这里只介绍正态总体的广义似然比检验问题 。 。
设 方差 方差 未知,检验问题是: 未知,检验问题是:

下面用广义似然比检验法导出合适的否定域。记 ,设 ,设 是样本 是样本 的值。 的值。 的似然函数 的似然函数

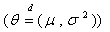 。易知 。易知


于是广义似然比

其中

显然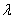 是 是 的严格增函数,故广义似然比检验的否定域为: 的严格增函数,故广义似然比检验的否定域为:
 (11) (11)
其中C适合  (一切 (一切 ) )
由概率统计知识知 时,统计量T服从n-1个自由度的t分布,故(11)中的C可从t分布表中查处,即 时,统计量T服从n-1个自由度的t分布,故(11)中的C可从t分布表中查处,即 ①。 ①。
三、实证研究
(一)数据的选取与处理
文章选用上证综指和深圳成指的收盘价作为分析对象,样本区间为2000年1月4日-2010年9月3日,共计2580个观测值。分别对两个指数的收盘价 进行对数差分处理即 进行对数差分处理即
 ,得到对数收益率序列向量记作 ,得到对数收益率序列向量记作 ,其中 ,其中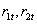 分别表示上证综指和深圳成指的对数收益率序列。 分别表示上证综指和深圳成指的对数收益率序列。
表1列出了这两个序列的几项描述性统计值,可以看出,在显著性水平 =0.05下,JB统计量显示拒绝沪深股市日收益率序列服从正态分布的原假设,并且从偏度和峰度看,收益分布具有明显的“尖峰厚尾”特征。 =0.05下,JB统计量显示拒绝沪深股市日收益率序列服从正态分布的原假设,并且从偏度和峰度看,收益分布具有明显的“尖峰厚尾”特征。
表1 上证综指和深圳成指日收益率的描述性统计值
|
|
均值
|
方差-协方差阵
|
相关矩阵
|
偏度
|
峰度
|
JB统计量
|
|
上综
|
深成
|
上综
|
深成
|
|
上综
深成
|
0.0246
|
2.9474
|
3.0131
|
1
|
0.9382
|
-0.0931
|
3.8907
|
1622.121
(0.0000)
|
|
0.0460
|
3.0131
|
3.4997
|
0.9382
|
1
|
-0.1261
|
3.2404
|
1129.214
(0.0000)
|
注:所有数据来源于RESSET金融数据库。
(二)模型的建立
由于我们主要关注波动率分析,因此设 为收益率序列向量去均值化后的残差序列向量,对两个残差序列进行ARCH效应检验(滞后阶数为2),结果如下表2所示。 为收益率序列向量去均值化后的残差序列向量,对两个残差序列进行ARCH效应检验(滞后阶数为2),结果如下表2所示。
表2ARCH效应检验结果
|
统计量 上综指 深成指
|
|
F-statistic 26.8905(0.0000) 33.9075(0.0000)
Obs*R-squared 52.7416(0.0000) 66.1512(0.0000)
|
注:括号中的数表示伴随概率,取显著性水平 =0.05。 =0.05。
从表2中可以发现,无论是F检验统计量还是LM统计量Obs*R-squared,其伴随概率均明显小于显著性水平 ,所以两个残差序列都具有条件异方差性,采用GARCH模型是合理的,故在这里 ,所以两个残差序列都具有条件异方差性,采用GARCH模型是合理的,故在这里 由MNM(2)-GARCH(1,1)模型(2)-(5)式确定。同时,文中虽然未给出具体模型形式,但仍考虑了BEKK、CCC、DCC模型做为对比模型。所有模型参数均通过MLE估计方法得到,具体结果见下表3。 由MNM(2)-GARCH(1,1)模型(2)-(5)式确定。同时,文中虽然未给出具体模型形式,但仍考虑了BEKK、CCC、DCC模型做为对比模型。所有模型参数均通过MLE估计方法得到,具体结果见下表3。
由表3可以看出,无论是对数似然函数值最大还是AIC、BIC值最小准则金融论文,MNM(2)-BEKK(1,1)在四个模型中均是最优的。具体来看此模型对沪深股市波动的刻画可以发现:首先,低波动率成分1伴随有正均值,高波动率成分2伴随有负均值,因此可以将低波动率成分1和高波动率成分2分别解释为牛市和熊市。其次,由于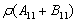 < < ② 所以具有较大混合权重的低波动率成分1是平稳的,而且波动具有较小的对冲击的反应参数和较大的持续参数,这说明低波动率成分即牛市中信息冲击对波动的影响程度较小但波动持续时间较长,即当前波动会对未来若干期的波动会产生持续影响,这可能是因为牛市时投资者相对独立,受利益驱动不会进行频繁交易,另外他们对市场信息的反应不够灵敏以及获取信息不够充分所导致的。同理,由于 ② 所以具有较大混合权重的低波动率成分1是平稳的,而且波动具有较小的对冲击的反应参数和较大的持续参数,这说明低波动率成分即牛市中信息冲击对波动的影响程度较小但波动持续时间较长,即当前波动会对未来若干期的波动会产生持续影响,这可能是因为牛市时投资者相对独立,受利益驱动不会进行频繁交易,另外他们对市场信息的反应不够灵敏以及获取信息不够充分所导致的。同理,由于 >1所以具有较小混合权重的高波动率成分2是非平稳的,但波动具有较大的反应参数和较小的持续参数,这说明高波动率成分即熊市中信息冲击对波动的影响程度较大但波动持续时间较短,这可能是因为大多数投资者属于风险规避型,微小的利空信息都会对其产生恐慌心理,结果大量跟风抛售,造成股市异常波动, >1所以具有较小混合权重的高波动率成分2是非平稳的,但波动具有较大的反应参数和较小的持续参数,这说明高波动率成分即熊市中信息冲击对波动的影响程度较大但波动持续时间较短,这可能是因为大多数投资者属于风险规避型,微小的利空信息都会对其产生恐慌心理,结果大量跟风抛售,造成股市异常波动,
2/3 首页 上一页 1 2 3 下一页 尾页 |


